题目内容
18. 如图,AB∥DC,∠A=90°,AE=DC.∠1=∠2
如图,AB∥DC,∠A=90°,AE=DC.∠1=∠2(1)△BEC是等腰直角三角形吗?并说明理由;
(2)若AB=6,BC=10$\sqrt{2}$,求四边形ABCD的面积.
分析 (1)首先证明Rt△ABE≌Rt△DEC可得∠AEB=∠ECD,BE=CE,再根据∠ECD+∠DEC=90°可得∠AEB+∠DEC=90°,进而可得∠BEC=90°,△BEC是等腰直角三角形;
(2)由△BEC是等腰直角三角形,BC=10$\sqrt{2}$,可求出BE=CE=10,又AB=6,可根据勾股定理得到AE=8,由Rt△ADE≌Rt△BEC,可知AB=DE=6,AE=CD=8,根据梯形面积公式计算即可.
解答 证明:(1)∵AB∥DC,
∴∠A+∠D=180°,
∵∠A=90°,
∴∠D=90°,
∴∠ECD+∠DEC=90°,
∵∠1=∠2,
∴BE=EC,
在Rt△ABE和Rt△DEC中,
$\left\{\begin{array}{l}{AE=DC}\\{BE=CE}\end{array}\right.$,
∴Rt△ABE≌Rt△DEC(HL),
∴∠AEB=∠ECD,
∴∠AEB+∠DEC=90°,
∴∠BEC=180°-90°=90°
∴△BEC是等腰直角三角形;
(2)∵△BEC是等腰直角三角形,BC=10$\sqrt{2}$,
∴BE=CE=10,
又∵AB=6,
∴在Rt△BAE中
AE=$\sqrt{B{E}^{2-}A{B}^{2}}$=8,
∵Rt△ADE≌Rt△BEC,
∴AB=DE=6,AE=CD=8,
∴四边形ABCD的面积=$\frac{1}{2}$×(AB+CD)×(AE+ED)=$\frac{1}{2}$×14×14=128.
点评 此题主要考查了全等三角形的判定与性质,关键是掌握证明三角形全等的判定方法:SSS、ASA、SAS、AAS、HL.

练习册系列答案
相关题目
13.在直角坐标系中,O为坐标原点,已知A(2,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
3.下列四边形中,两条对角线一定不相等的是( )
| A. | 平行四边形 | B. | 矩形 | C. | 等腰梯形 | D. | 直角梯形 |
8. 如图,在⊙O中,∠ACB=32°,则∠AOB的度数是( )
如图,在⊙O中,∠ACB=32°,则∠AOB的度数是( )
 如图,在⊙O中,∠ACB=32°,则∠AOB的度数是( )
如图,在⊙O中,∠ACB=32°,则∠AOB的度数是( )| A. | 16° | B. | 32° | C. | 64° | D. | 74° |
 如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,则∠AEB=36°.
如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,则∠AEB=36°.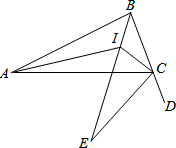 如图,△ABC中,AI、BI分别平分∠BAC、∠ABC,CE是△ABC的外角∠ACD的平分线,交BI延长线于E,连结CI,若AB=1,且△ABC与△ICE相似,那么AC=$\frac{1}{2}$或1或2.
如图,△ABC中,AI、BI分别平分∠BAC、∠ABC,CE是△ABC的外角∠ACD的平分线,交BI延长线于E,连结CI,若AB=1,且△ABC与△ICE相似,那么AC=$\frac{1}{2}$或1或2.