题目内容
8．
如图，在⊙O中，∠ACB=32°，则∠AOB的度数是（ ）| A． | 16° | B． | 32° | C． | 64° | D． | 74° |
分析 直接利用圆周角定理解答即可．
解答 解：∵圆心角∠AOB和圆周角∠ACB所对的弧相同，
∴∠AOB=2∠ACB=64°．
故选：C．
点评 本题主要考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
如图，AB∥DC，∠A=90°，AE=DC．∠1=∠2
16．下列多项式相乘，不能用平方差公式计算的是（ ）
| A． | （x-2y）（2y-x） | B． | （x-2y）（-x-2y） | C． | （2y-x）（x+2y） | D． | （2y-x）（-x-2y） |
3．
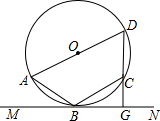如图所示，已知四边形ABCD为圆内接四边形，AD为圆的直径，直线MN切圆于点B，DC的延长线交MN于G，且cos∠ABM=$\frac{{\sqrt{3}}}{2}$，则tan∠BCG的值为（ ）
如图所示，已知四边形ABCD为圆内接四边形，AD为圆的直径，直线MN切圆于点B，DC的延长线交MN于G，且cos∠ABM=$\frac{{\sqrt{3}}}{2}$，则tan∠BCG的值为（ ）| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | 1 | D． | $\sqrt{3}$ |
20．下列从左到右的变形中，是因式分解的是（ ）
| A． | x2-6x+9=x（x-6-9） | B． | （a+2）（a-2）=a2-4 | C． | 2a（b-c）=2ab-2bc | D． | y2-4y+4=（y-2）2 |
17．
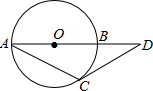如图，已知⊙O的半径为R，AB是⊙O的直径，D是AB延长线上一点，DC是⊙O的切线，C是切点，连结AC．若∠CAB=30°，则BD的长为（ ）
如图，已知⊙O的半径为R，AB是⊙O的直径，D是AB延长线上一点，DC是⊙O的切线，C是切点，连结AC．若∠CAB=30°，则BD的长为（ ）| A． | R | B． | $\sqrt{3}$R | C． | 2R | D． | $\frac{\sqrt{3}}{2}$R |
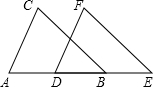把下面的推理过程补充完整，并在括号内注明理由．如图，点B、D在线段AE上，BC∥EF，AD=BE，BC=EF，试说明：（1）∠C=∠F；（2）AC∥DF．