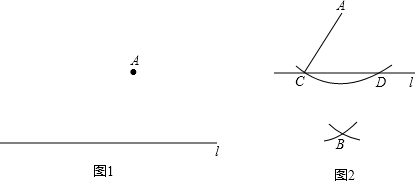题目内容
19.先化简,再求值:(1-$\frac{3}{x+1}$)÷$\frac{{x}^{2}-4x+4}{x+1}$,其中x=-$\frac{1}{2}$.分析 根据分式的减法和除法可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:(1-$\frac{3}{x+1}$)÷$\frac{{x}^{2}-4x+4}{x+1}$
=$\frac{x+1-3}{x+1}•\frac{x+1}{(x-2)^{2}}$
=$\frac{x-2}{x+1}•\frac{x+1}{(x-2)^{2}}$
=$\frac{1}{x-2}$,
当x=-$\frac{1}{2}$时,原式=$\frac{1}{-\frac{1}{2}-2}=-\frac{2}{5}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
11.计算正确的是( )
| A. | 3.4×104=340000 | B. | m×2m2=3m2 | C. | (-$\frac{1}{2}$mn2)2=m2n4 | D. | 4xy-4yx=0 |
 尺规作图:请在原图上作一个∠AOC,使∠AOC=2∠AOB,不写已知、求作和作法,保留作图痕迹,在所作图中标上必要的字母.
尺规作图:请在原图上作一个∠AOC,使∠AOC=2∠AOB,不写已知、求作和作法,保留作图痕迹,在所作图中标上必要的字母.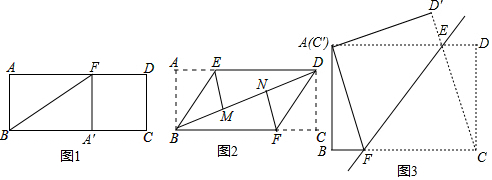
 如图,四边形ABCD是平行四边形,对角线AC,BD交于点O,且△OAB为等边三角形.求证:四边形ABCD为矩形.
如图,四边形ABCD是平行四边形,对角线AC,BD交于点O,且△OAB为等边三角形.求证:四边形ABCD为矩形.