题目内容
15. 如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=62°,那么∠BOD=( )
如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=62°,那么∠BOD=( )| A. | 124° | B. | 100° | C. | 62° | D. | 31° |
分析 由圆内接四边形的外角等于它的内对角知,∠A=∠DCE=62°,由圆周角定理知,∠BOD=2∠A=124°.
解答 解:∵四边形ABCD内接于⊙O,
∴∠A=∠DCE=62°,
∴∠BOD=2∠A=124°.
故选A.
点评 本题利用了圆内接四边形的性质和圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
6.关于x的一元二次方程(a-2)x2+x+a2-4=0的一个根是0,则a的值为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 一元二次方程 |
10.关于x的分式方程$\frac{x-a}{x-1}$-$\frac{3}{x}$=1无解,则a的值( )
| A. | a=1 | B. | a=-2 或a=1 | C. | a=-5 | D. | a=-2或a=-5 |
20.以下各组线段长为边,能组成直角三角形的是( )
| A. | 1,4,4 | B. | 1,2,3 | C. | 9,12,15 | D. | 4,5,6 |
4. 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )| A. | $\sqrt{13}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 5 |
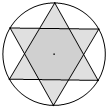 如图所示的“六芒星”图标是由圆的六等分点连接而成,若圆的半径为2$\sqrt{3}$,则图中阴影部分的面积为12$\sqrt{3}$.
如图所示的“六芒星”图标是由圆的六等分点连接而成,若圆的半径为2$\sqrt{3}$,则图中阴影部分的面积为12$\sqrt{3}$.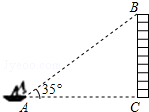 如图,从一艘船的点A处观测海岸上高为41m的灯塔BC(观测点A与灯塔底部C在一个水平面上),测得灯塔顶部B的仰角为35°,则观测点A到灯塔BC的距离为59m.(精确到1m)
如图,从一艘船的点A处观测海岸上高为41m的灯塔BC(观测点A与灯塔底部C在一个水平面上),测得灯塔顶部B的仰角为35°,则观测点A到灯塔BC的距离为59m.(精确到1m)