题目内容
1．
如图，在△ABC中，点D、E分别在AB、AC上，∠ADE=∠C，求证：AD•AB=AE•AC．
分析 只要证明△ADE∽△ACB即可解决问题．
解答 证明：∵∠A=∠A，∠ADE=∠C，
∴△ADE∽△ACB，
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$，
∴AD•AB=AE•AC．
点评 本题考查相似三角形的判定和性质等知识，正确寻找相似三角形是解题的关键，属于中考常考题型．
练习册系列答案
相关题目
12．若ax=6，ay=4，则a2x-y的值为（ ）
| A． | 8 | B． | 9 | C． | 32 | D． | 40 |
16．将抛物线y=-2（x+1）2-2向左平移2个单位，向下平移3个单位后的新抛物线解析式为（ ）
| A． | y=-2（x-1）2+1 | B． | y=-2（x+3）2-5 | C． | y=-2（x-1）2-5 | D． | y=-2（x+3）2+1 |
10．
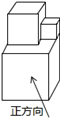如图是三个大小不等的正方体拼成的几何体，其中两个较小正方体的棱长之和等于大正方体的棱长，从正面、左面、上面看该几何体，所看到的图形的面积分别是S1，S2，S3，则S1，S2，S3的大小关系是（ ）
如图是三个大小不等的正方体拼成的几何体，其中两个较小正方体的棱长之和等于大正方体的棱长，从正面、左面、上面看该几何体，所看到的图形的面积分别是S1，S2，S3，则S1，S2，S3的大小关系是（ ）| A． | S1＞S2＞S3 | B． | S3＞S2＞S1 | C． | S2＞S3＞S1 | D． | S1＞S3＞S2 |