题目内容
已知α、β是关于x的一元二次方程x2+(2m+3)x+m2=0的两个不相等的实数根,且满足β=-α(1+β),则m的值是 .
考点:根与系数的关系
专题:计算题
分析:先根据判别式的意义得到m>-
,再根据根与系数的关系得+β=-(2m+3),αβ=m2,由于β=-α(1+β),即α+β+αβ=0,所以-(2m+3)+m2=0,解得m1=-1,m2=3,然后根据m的取值范围确定m的值.
| 3 |
| 4 |
解答:解:根据题意得△=(2m+3)2-4m2>0,解得m>-
,
α+β=-(2m+3),αβ=m2,
∵β=-α(1+β),即α+β+αβ=0,
∴-(2m+3)+m2=0,即m2-2m-3=0,解得m1=-1,m2=3,
而m>-
,
∴m=3.
故答案为3.
| 3 |
| 4 |
α+β=-(2m+3),αβ=m2,
∵β=-α(1+β),即α+β+αβ=0,
∴-(2m+3)+m2=0,即m2-2m-3=0,解得m1=-1,m2=3,
而m>-
| 3 |
| 4 |
∴m=3.
故答案为3.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
某班级第一小组7名同学积极捐出自己的零花钱支持地震灾区,他们捐款的数额分别是(单位:元)100,40,100,60,50,100,200,这组数据的众数和中位数分别是( )
| A、100元,40元 |
| B、100元,60元 |
| C、200元,100元 |
| D、100元,100元 |

 如图,矩形ABCD的顶点A、D在反比例函数
如图,矩形ABCD的顶点A、D在反比例函数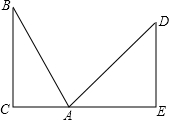 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点,当它靠在另一侧墙时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离DE=3
如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点,当它靠在另一侧墙时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°.点D到地面的垂直距离DE=3 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.