Question

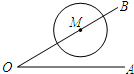已知∠AOB=30°，M为OB上一点，且OM=5cm，以M为圆心，r为半径画圆．若C是OA上一点，OC等于5cm，讨论OC与⊙M的公共点个数，并写出r相应的取值范围．

Answer 1

考点：直线与圆的位置关系

专题：

分析：作MN⊥OA于N，如图，根据含30度的直角三角形三边的关系得到MN=

1

2

OM=

5

2

，然后根据直线与圆的关系得到当r=

5

2

时，⊙M与射线OC相切，只有一个公共点；当0＜r＜

5

2

时，⊙M与射线OC相离，没有公共点；当

5

2

＜r≤5时，⊙M与射线OC有两个公共点，而当r＞5时，⊙M与射线OC只有一个公共点．

解答：解：作MN⊥OA于N，如图，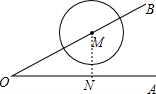
∵∠AOB=30°，
∴MN=

1

2

OM=

1

2

×5=

5

2

，
∴当r=

5

2

时，⊙M与射线OC只有一个公共点；
当0＜r＜

5

2

时，⊙M与射线OC没有公共点；
当

5

2

＜r≤5时，⊙M与射线OC有两个公共点；
当r＞5时，⊙M与射线OC只有一个公共点．
所以当0＜r＜

5

2

时，⊙M与射线OC没有公共点；当r=

5

2

或r＞5时，⊙M与射线OC只有一个公共点；当

5

2

＜r≤5时，⊙M与射线OC有两个公共点．

点评：本题考查了直线和圆的位置关系：设⊙O的半径为r，圆心O到直线l的距离为d．若直线l和⊙O相交?d＜r；直线l和⊙O相切?d=r；直线l和⊙O相离?d＞r．