题目内容
先化简,再求代数式(
+
)÷
的值,其中x=
cos30°.
| 1 |
| x |
| x+1 |
| x |
| x+2 |
| x2+x |
| 3 |
考点:分式的化简求值,特殊角的三角函数值
专题:计算题
分析:原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答:解:原式=
•
=x+1,
当x=
×
=
时,原式=
.
| x+2 |
| x |
| x(x+1) |
| x+2 |
当x=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
用配方法解下列方程,配方正确的是( )
| A、2y2-4y-4=0可化为(y-1)2=4 |
| B、x2-2x-9=0可化为(x-1)2=8 |
| C、x2+8x-9=0可化为(x+4)2=16 |
| D、x2-4x=0可化为(x-2)2=4 |
在一个由8×8个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为S1,把圆周经过的所有小方格的圆外部分的面积之和记为S2,则
的整数部分是 .
| S1 |
| S2 |
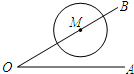 已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,r为半径画圆.若C是OA上一点,OC等于5cm,讨论OC与⊙M的公共点个数,并写出r相应的取值范围.
已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,r为半径画圆.若C是OA上一点,OC等于5cm,讨论OC与⊙M的公共点个数,并写出r相应的取值范围.