题目内容
试求满足
+
+
=
,且x-y最大的正整数组(x,y)(x>y>2014).
| 1 |
| x |
| 1 |
| y |
| 1 |
| xy |
| 1 |
| 2014 |
考点:非一次不定方程(组),质因数分解
专题:
分析:可将原方程转化为(x-2014)(y-2014)=2014×2015,由x>y>2014可得x-2014>y-2014>0,由x-y最大可得(x-2014)-(y-2014)最大,再由x、y都是正整数可得x-2014是2014×2015最大的正约数,y-2014是2014×2015最小的正约数,从而可求出x、y的值,就可解决问题.
解答:解:等式两边同乘以2014xy得:
2014y+2014x+2014=xy,
∴xy-2014x-2014y=2014,
∴(x-2014)(y-2014)=20142+2014,
∴(x-2014)(y-2014)=2014×2015.
∵x>y>2014,
∴x-2014>y-2014>0,
∵x-y最大,
∴(x-2014)-(y-2014)=x-y最大.
又∵x、y都是正整数,
∴x-2014=2014×2015,y-2014=1,
∴x=2014×2016=4060224,y=2015.
∴符合要求的正整数组为(4060224,2015).
2014y+2014x+2014=xy,
∴xy-2014x-2014y=2014,
∴(x-2014)(y-2014)=20142+2014,
∴(x-2014)(y-2014)=2014×2015.
∵x>y>2014,
∴x-2014>y-2014>0,
∵x-y最大,
∴(x-2014)-(y-2014)=x-y最大.
又∵x、y都是正整数,
∴x-2014=2014×2015,y-2014=1,
∴x=2014×2016=4060224,y=2015.
∴符合要求的正整数组为(4060224,2015).
点评:本题考查的是解非一次不定方程、质因数分解等知识,而将方程转化为两个因式的乘积等于一个正整数是解决本题的关键.

练习册系列答案
相关题目
用配方法解下列方程,配方正确的是( )
| A、2y2-4y-4=0可化为(y-1)2=4 |
| B、x2-2x-9=0可化为(x-1)2=8 |
| C、x2+8x-9=0可化为(x+4)2=16 |
| D、x2-4x=0可化为(x-2)2=4 |
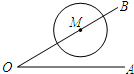 已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,r为半径画圆.若C是OA上一点,OC等于5cm,讨论OC与⊙M的公共点个数,并写出r相应的取值范围.
已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心,r为半径画圆.若C是OA上一点,OC等于5cm,讨论OC与⊙M的公共点个数,并写出r相应的取值范围.