题目内容
11. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=30°.
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=30°.
分析 首先证明∠ACC′=∠AC′C;然后运用三角形的内角和定理求出∠CAC′=30°即可解决问题.
解答 解:由题意得:
AC=AC′,
∴∠ACC′=∠AC′C;
∵CC′∥AB,且∠BAC=75°,
∴∠ACC′=∠AC′C=∠BAC=75°,
∴∠CAC′=180°-2×75°=30°;
由题意知:∠BAB′=∠CAC′=30°,
故答案为30°.
点评 此题主要考查了旋转的性质以及平行线的性质,得出AC=AC′,∠BAC=∠ACC′=75°是解题关键.

练习册系列答案
相关题目
19.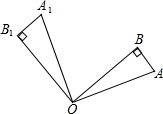 如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
 如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )| A. | 125° | B. | 65° | C. | 75° | D. | 50° |
1.函数y=$\frac{\sqrt{x}}{1-x}$的自变量x的取值范围是( )
| A. | x≥0 | B. | x≠1 | C. | x>1 | D. | x≥0且x≠1 |
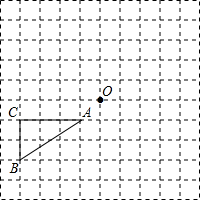 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC.点A、B、C、O均在小正方形的顶点上.
如图,在每个小正方形的边长均为1个单位长度的方格纸中,有△ABC.点A、B、C、O均在小正方形的顶点上. 如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=$\frac{3}{5}$,AB=4.
如图,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=$\frac{3}{5}$,AB=4. 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°.
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB+∠EDC=120°. 如图,直线AB,CD交于点O,OE⊥AB,若∠AOD=50°,则∠COE的度数为40°.
如图,直线AB,CD交于点O,OE⊥AB,若∠AOD=50°,则∠COE的度数为40°.