题目内容
12. 如图,正方形ABCD的边长为4,正方形ECFG的边长为8,则阴影部分的周长为32.1,面积为24.(精确到0.1)
如图,正方形ABCD的边长为4,正方形ECFG的边长为8,则阴影部分的周长为32.1,面积为24.(精确到0.1)
分析 根据勾股定理求出BD、BG,即可求出阴影部分的周长;延长BA、GE相交于点H,用△BGH的面积-△ABD的面积-正方形ADEH的面积即可得出阴影部分的面积.
解答 解:∵四边形ABCD和四边形ECFG是正方形,
∴AB=AD=BC=4,∠A=90°,CF=FG=GE=8,∠F=90°,
∴DE=8-4=4,BD=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,BF=4+8=12,
∴BG=$\sqrt{1{2}^{2}+{8}^{2}}$=4$\sqrt{13}$,
∴阴影部分的周长为:
BD+BG+GE+DE=4$\sqrt{2}$+4$\sqrt{13}$+8+4≈32.1;
延长BA、GE相交于点H;如图所示: 得∠H=90°,四边形ADEH是正方形;
得∠H=90°,四边形ADEH是正方形;
∴阴影部分的面积=S△BGH-S△ABD-S正方形ADEH
=$\frac{1}{2}$×12×8-$\frac{1}{2}$×4×4-4×4
=24;
故答案为:32.1;24.
点评 本题考查了正方形的性质、面积的求法以及三角形的面积、阴影面积的求法;根据勾股定理求边长和阴影面积的间接求法是解题的关键.

练习册系列答案
相关题目
20.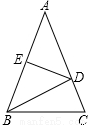 如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )
如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )
 如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )
如图,在△ABC中,AB=AC=20cm,DE是AB的垂直平分线,若△BCD的周长为35cm,则BC的长为( )| A. | 15cm | B. | 10cm | C. | 8cm | D. | 5cm |
7.已知两个相似多边形的面积比是9:16,其中较小多边形的周长为36cm,则较大多边形的周长为( )
| A. | 48cm | B. | 54cm | C. | 56cm | D. | 64cm |
17.下列运算正解的是( )
| A. | $\sqrt{5}$+$\sqrt{7}$=$\sqrt{12}$ | B. | 5+$\sqrt{2}$=5$\sqrt{2}$ | C. | $\sqrt{3}$×$\sqrt{6}$=3$\sqrt{2}$ | D. | $\sqrt{{(-2)}^{2}}$=-2 |
1. △ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的度数是( )
△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的度数是( )
 △ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的度数是( )
△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的度数是( )| A. | 20° | B. | 30° | C. | 45° | D. | 60° |
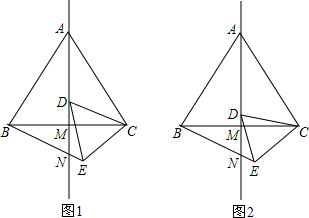
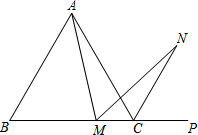 如图,在等边△ABC中,M为BC边上任意一点(不含B、C两点),P为BC延长线上一点,N是∠ACP的平分线上一点.已知∠AMN=60°,求证:AM=NM.
如图,在等边△ABC中,M为BC边上任意一点(不含B、C两点),P为BC延长线上一点,N是∠ACP的平分线上一点.已知∠AMN=60°,求证:AM=NM.