题目内容
17.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点(2,-1),则该反比例函数的图象在( )| A. | 第一、二象限 | B. | 笫一、三象限 | C. | 笫二、三象限 | D. | 第二、四象限 |
分析 先把点(2,-1)代入反比例函数求出k的值,再由反比例函数的图象与系数的关系即可得出结论.
解答 解:∵反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点(2,-1),
∴k=2×(-1)=-2<0,
∴该反比例函数的图象的两个分支分别位于二四象限.
故选D.
点评 本题考查的是反比例函数的性质,熟知反比例函数的图象与系数的关系是解答此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
8. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,0),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,6),B(8,0),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C的坐标为( )
 如图,线段AB两个端点的坐标分别为A(6,6),B(8,0),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,6),B(8,0),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C的坐标为( )| A. | (3,0) | B. | (4,0) | C. | (3,3) | D. | (4,3) |
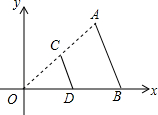
5. 如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m-n等于( )
如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m-n等于( )
 如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m-n等于( )
如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m-n等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 无法确定 |
12. 如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
 如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )| A. | 不变 | B. | 增大 | C. | 减小 | D. | 先变大再变小 |
2.为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口的费用(元/吨)如表所示:
(1)设从甲仓库运送到A港口的物资为x吨,求总运费y(元)与x(吨)之间的函数关系式,并写出x的取值范围;
(2)求出最低费用,并说明费用最低时的调配方案.
| 港口 | 运费(元/吨) | |
| 甲库 | 乙库 | |
| A港 | 14 | 20 |
| B港 | 10 | 8 |
(2)求出最低费用,并说明费用最低时的调配方案.
6.(-2)×3的结果是( )
| A. | 6 | B. | -6 | C. | 1 | D. | -5 |
7.-$\sqrt{5}$的绝对值是( )
| A. | -$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
 如图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120),已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.
如图中的折线ABC表示某汽车的耗油量y(单位:L/km)与速度x(单位:km/h)之间的函数关系(30≤x≤120),已知线段BC表示的函数关系中,该汽车的速度每增加1km/h,耗油量增加0.002L/km.