题目内容
15．已知二次函数y=x2-2x．（1）写出它的对称轴和顶点坐标．
（2）写出将抛物线y=x2-2x关于y轴对称后的解析式．
分析 （1）利用配方法解答即可；
（2）关于y轴对称后的解析式a值不变，b变为原来的相反数．
解答 解：（1）∵y=x2-2x=x2-2x+1-1=（x-1）2-1，
∴对称轴为x=1，顶点坐标为（1，-1）．
（2）∵将抛物线y=x2-2x关于y轴对称后的抛物线的顶点为（-1，-1），
∴抛物线的解析式为y=x2+2x．
点评 本题主要考查的是二次函数的性质，掌握二次函数的性质是解题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
6．下面各式运用等式的性质变形，错误的是（ ）
| A． | 若x-3=y-3，则x=y | B． | 若$\frac{x}{a}$=$\frac{y}{a}$，则x=y | ||
| C． | 若a（c2+1）=b（c2+1），则a=b | D． | 若ac=bc，则a=b |
已知：如图，AB=AD，AC=AE，且BA⊥AC，DA⊥AE．求证：
20．
有理数a、b在数轴上对应的位置如图所示，其中正确的结论是（ ）
有理数a、b在数轴上对应的位置如图所示，其中正确的结论是（ ）| A． | a+b＞0 | B． | |a|＞|b|＞0 | C． | ab＜0 | D． | a2＞b2 |
7．
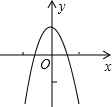二次函数y=-3x2+1的图象如图所示，将其沿x轴翻折后得到的抛物线的解析式为（ ）
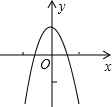二次函数y=-3x2+1的图象如图所示，将其沿x轴翻折后得到的抛物线的解析式为（ ）| A． | y=-3x2-1 | B． | y=3x2 | C． | y=3x2+1 | D． | y=3x2-1 |