题目内容
12.解方程组:$\left\{\begin{array}{l}{5x-4y=0}\\{3y-5z=0}\\{2x-y+z=6}\end{array}\right.$.分析 方程组利用代入消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{5x-4y=0①}\\{3y-5z=0②}\\{2x-y+z=6③}\end{array}\right.$,
由①得:y=$\frac{5}{4}$x④,
由②得:z=$\frac{3}{5}$y=$\frac{3}{4}$x⑤,
把④,⑤代入③得:2x-$\frac{5}{4}$x+$\frac{3}{4}$x=6,即x=4,
把x=4代入④得:y=5,
把x=4代入⑤得:z=3,
则方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=5}\\{z=3}\end{array}\right.$.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
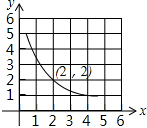 已知反比例函数y=$\frac{k}{x}$的图象经过点(2,2).
已知反比例函数y=$\frac{k}{x}$的图象经过点(2,2). 如图,?ABCD中,P是AC,BD交于点O,P是?ABCD外一点,且∠APC=∠BPD=90°,求证:?ABCD是矩形.
如图,?ABCD中,P是AC,BD交于点O,P是?ABCD外一点,且∠APC=∠BPD=90°,求证:?ABCD是矩形.