题目内容
1. 如图,?ABCD中,P是AC,BD交于点O,P是?ABCD外一点,且∠APC=∠BPD=90°,求证:?ABCD是矩形.
如图,?ABCD中,P是AC,BD交于点O,P是?ABCD外一点,且∠APC=∠BPD=90°,求证:?ABCD是矩形.
分析 连接PO,首先根据O为BD和AC的中点,在Rt△APC中PO=$\frac{1}{2}$AC,在Rt△PBD中,PO=$\frac{1}{2}$BD,进而得到AC=BD,再根据对角线相等的平行四边形是矩形可证出结论.
解答 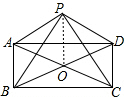 证明:连接PO,
证明:连接PO,
∵O是AC、BD的中点,
∴AO=CO,BO=DO,
在Rt△PBD中,
∵O为BD中点,
∴PO=$\frac{1}{2}$BD,
在Rt△APC中,
∵O为AC中点,
∴PO=$\frac{1}{2}$AC,
∴AC=BD,
又∵四边形ABCD是平行四边形,
∴平行四边形ABCD是矩形.
点评 此题主要考查了矩形的判定,关键是掌握直角三角形斜边上的中线等于斜边的一半,正确的作出辅助线是解决本题的另一个关键点.

练习册系列答案
相关题目
 如图,圆内接四边形ABCD中,AB=AD,∠BAD=60°,则∠ACD度数是60°.
如图,圆内接四边形ABCD中,AB=AD,∠BAD=60°,则∠ACD度数是60°.