题目内容
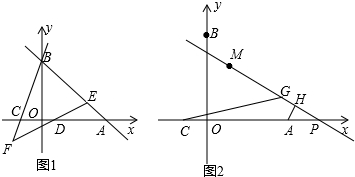
14. 已知A地在B地的正南方向3km处,甲、乙两人分别从两地向正北方向匀速直行,他们与A地距离s(千米)与所行时间t(小时)之间的关系如图所示,其中l1表示甲运动的过程,l2表示乙运动的过程,根据图象回答:
已知A地在B地的正南方向3km处,甲、乙两人分别从两地向正北方向匀速直行,他们与A地距离s(千米)与所行时间t(小时)之间的关系如图所示,其中l1表示甲运动的过程,l2表示乙运动的过程,根据图象回答:(1)开始时,甲、乙两人谁在A地?谁在B地;
(2)追及者何时追上被追着?此时追及者已走了多少路程;
(3)甲、乙两人行走的速度各是多少;
(4)写出l1,l2对应的函数表达式,不用写出自变量的取值范围.
分析 (1)根据题意及函数图象就可以得出甲、乙的位置;
(2)由图象可得出追及者甲用了2小时追上乙,此时甲走了6千米;
(3)由图象可知,甲2小时走了6千米,乙2小时走了3千米,根据速度=路程÷时间即可求解;
(4)运用待定系数法可求出l1,l2对应的函数表达式.
解答 解:(1)由题意,可得开始时,甲在A地,乙在B地;
(2)由图象可得:
追及者甲用了2小时追上乙,此时甲走了6千米;
(3)由图象可知,甲2小时走了6千米,乙2小时走了3千米,
所以甲行走的速度为:6÷2=3千米/时,乙行走的速度为:3÷2=1.5千米/时;
(4)设l1的解析式为S=kt,
由题意得:6=2k,
解得:k=3,
所以l1的解析式为S=3t;
设l2的解析式为S=mt+n,
由题意得:$\left\{\begin{array}{l}{n=3}\\{2m+n=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=1.5}\\{n=3}\end{array}\right.$,
所以l2的解析式为S=1.5t+3.
点评 本题考查了一次函数的运用,待定系数法求直线解析式的应用,解答本题时读懂函数图象从图象中获取有用信息是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 如图,AB是⊙O的直径,点C在⊙O上,直线AB与过点C的切线交于点E,连接BC,AC,过点O作OD∥BC与直线CE交于点D,连接DA.
如图,AB是⊙O的直径,点C在⊙O上,直线AB与过点C的切线交于点E,连接BC,AC,过点O作OD∥BC与直线CE交于点D,连接DA.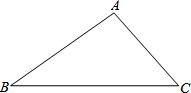 如图,△ABC中,∠B=30°,∠BAC=105°,AB=24,求△ABC的面积.
如图,△ABC中,∠B=30°,∠BAC=105°,AB=24,求△ABC的面积.