题目内容
3. 如图,MN∥BC,∠AEN=100°,∠B=65°,则∠A=35°.
如图,MN∥BC,∠AEN=100°,∠B=65°,则∠A=35°.
分析 根据邻补角的定义求出∠CEN,再根据两直线平行,内错角相等求出∠C,然后利用三角形的内角和定理列式计算即可得解.
解答 解:∵∠AEN=100°,
∴∠CEN=180°-∠AEN=180°-100°=80°,
∵MN∥BC,
∴∠C=∠CEN=80°,
在△ABC中,∠A=180°-∠B-∠C=180°-65°-80°=35°.
故答案为:35.
点评 本题考查了平行线的性质,三角形的内角和定理,邻补角的定义,是基础题,熟记性质并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
13.下列说法正确的有( )个
(1)25的立方根是5;
(2)互为相反数的两个数,它们的立方根也互为相反数;
(3)任何数的立方根只有一个;
(4)如果一个数的平方根与其立方根相同,则这个数是1.
(1)25的立方根是5;
(2)互为相反数的两个数,它们的立方根也互为相反数;
(3)任何数的立方根只有一个;
(4)如果一个数的平方根与其立方根相同,则这个数是1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.若分式$\frac{2x-y}{y}$中的x,y的值变为原来的2倍,则此分式的值( )
| A. | 不变 | B. | 发生变化 | C. | 是原来的2倍 | D. | 是原来的$\frac{1}{2}$ |
18.(2+1)(22+1)(24+1)(28+1)…(232+1)+1 的个位数字为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
15. 如图所示的解集,正确的是( )
如图所示的解集,正确的是( )
 如图所示的解集,正确的是( )
如图所示的解集,正确的是( )| A. | x<-2 | B. | x≤-2 | C. | x>-2 | D. | x≥-2 |
 如图,在小正方形边长均为单位1的方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
如图,在小正方形边长均为单位1的方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.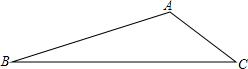 △ABC是武汉市在拆除违章建筑后的一块三角形空地,已知∠A=150°,AB=30m,AC=20m,如果要在这块空地上种草皮,按每平方米a元计算,则需要资金多少元?
△ABC是武汉市在拆除违章建筑后的一块三角形空地,已知∠A=150°,AB=30m,AC=20m,如果要在这块空地上种草皮,按每平方米a元计算,则需要资金多少元?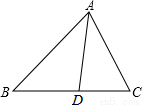 如图,△ABC中,AD是∠BAC的角平分线,AB=4,AC=3,则△ABD与△ADC的面积比是4:3.
如图,△ABC中,AD是∠BAC的角平分线,AB=4,AC=3,则△ABD与△ADC的面积比是4:3.