题目内容
14.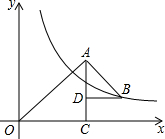 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{6}{x}$在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC-S△BAD为( )
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{6}{x}$在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC-S△BAD为( )| A. | 36 | B. | 12 | C. | 6 | D. | 3 |
分析 设△OAC和△BAD的直角边长分别为a、b,结合等腰直角三角形的性质及图象可得出点B的坐标,根据三角形的面积公式结合反比例函数系数k的几何意义以及点B的坐标即可得出结论.
解答 解:设△OAC和△BAD的直角边长分别为a、b,
则点B的坐标为(a+b,a-b).
∵点B在反比例函数y=$\frac{6}{x}$的第一象限图象上,
∴(a+b)×(a-b)=a2-b2=6.
∴S△OAC-S△BAD=$\frac{1}{2}$a2-$\frac{1}{2}$b2=$\frac{1}{2}$(a2-b2)=$\frac{1}{2}$×6=3.
故选D.
点评 本题考查了反比例函数系数k的几何意义、等腰三角形的性质以及面积公式,解题的关键是找出a2-b2的值.本题属于基础题,难度不大,解决该题型题目时,设出等腰直角三角形的直角边,用其表示出反比例函数上点的坐标是关键.

练习册系列答案
相关题目
9.已知地球上海洋面积为316 000 000km2,数据316 000 000用科学记数法表示为( )
| A. | 3.61×109 | B. | 3.61×108 | C. | 3.61×107 | D. | 3.61×106 |
6.下列特征量不能反映一组数据集中趋势的是( )
| A. | 众数 | B. | 中位数 | C. | 方差 | D. | 平均数 |
3.下列算式中,结果等于a6的是( )
| A. | a4+a2 | B. | a2+a2+a2 | C. | a2•a3 | D. | a2•a2•a2 |
4.使二次根式$\sqrt{x-1}$有意义的x的取值范围是( )
| A. | x≠1 | B. | x>1 | C. | x≤1 | D. | x≥1 |
 如图,点P在反比例函数$y=\frac{k}{x}$的图象上,且PD⊥x轴于点D,连接OP,若△POD的面积为6,则k的值是( )
如图,点P在反比例函数$y=\frac{k}{x}$的图象上,且PD⊥x轴于点D,连接OP,若△POD的面积为6,则k的值是( )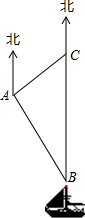 南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+$\sqrt{3}$)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+$\sqrt{3}$)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.