题目内容
15.若反比例函数y=$\frac{k}{x}$(k≠0)的图象过点(2,1),则这个函数的图象还经过的点是( )| A. | (-2,1) | B. | (-l,2) | C. | (-2,-1) | D. | (1,-2) |
分析 先把点(2,1)代入反比例函数y=$\frac{k}{x}$(k≠0),求出k的值,再对各选项进行逐一判断即可.
解答 解:∵反比例函数y=$\frac{k}{x}$(k≠0)的图象过点(2,1),
∴k=2×1=2.
A、∵(-2)×1=-2≠2,∴此点不在函数图象上,故本选项不合题意;
B、∵(-1)×2=-2≠2,∴此点不在函数图象上,故本选项不合题意;
C、∵(-2)×(-1)=2,∴此点在函数图象上,故本选项符合题意;
D、∵1×(-2)=-2≠2,∴此点不在函数图象上,故本选项不合题意.
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.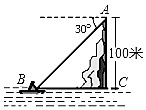 如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )
如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )
 如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )
如图,在高出海平面100m的悬崖顶A处,观测海面上的一艘小船B,并测得它的俯角为30°,则船与观测者之间的水平距离为( )| A. | 50$\sqrt{3}$ | B. | 100 | C. | 100+$\sqrt{3}$ | D. | 100$\sqrt{3}$ |
7. 如图,在数轴上,点A表示$\sqrt{2}$,点B表示5.1,则A,B之间表示整数的点共有( )
如图,在数轴上,点A表示$\sqrt{2}$,点B表示5.1,则A,B之间表示整数的点共有( )
 如图,在数轴上,点A表示$\sqrt{2}$,点B表示5.1,则A,B之间表示整数的点共有( )
如图,在数轴上,点A表示$\sqrt{2}$,点B表示5.1,则A,B之间表示整数的点共有( )| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
4.若等腰三角形中有两边长分别为3和7,则这个三角形的周长为( )
| A. | 13 | B. | 17 | C. | 10或13 | D. | 13或17 |
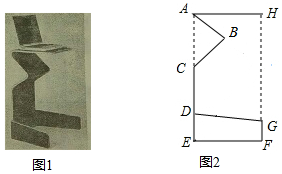 如图1是一张创意电脑桌,图2是其平面示意图,已知以A、E、F、H为顶点的四边形,点C、D在AE上,点G在HF上,测得AC=CD=2DE,DE=$\frac{4}{3}$GF,AB=CB=31.2cm,AH=50cm,∠BAH=40°.
如图1是一张创意电脑桌,图2是其平面示意图,已知以A、E、F、H为顶点的四边形,点C、D在AE上,点G在HF上,测得AC=CD=2DE,DE=$\frac{4}{3}$GF,AB=CB=31.2cm,AH=50cm,∠BAH=40°. 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后楼梯AC长为2$\sqrt{6}$米.
如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后楼梯AC长为2$\sqrt{6}$米.