题目内容
16.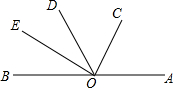 如图,已知AB是一条直线,OC是∠AOD的平分线,OE是∠BOD的平分线,若∠AOE=140°,求∠BOE及∠AOC的度数.
如图,已知AB是一条直线,OC是∠AOD的平分线,OE是∠BOD的平分线,若∠AOE=140°,求∠BOE及∠AOC的度数.
分析 根据邻补角定义可得∠BOE=180°-∠AOE=40°;由角平分线定义求出∠BOD=2∠BOE=80°,根据邻补角定义可得∠AOD=180°-∠BOD=100°,再根据角平分线定义即可求出∠AOC=$\frac{1}{2}$∠AOD=50°.
解答 解:∵AB是一条直线,∠AOE=140°,
∴∠BOE=180°-∠AOE=40°,
∵OE是∠BOD的平分线,
∴∠BOD=2∠BOE=80°,
∴∠AOD=180°-∠BOD=100°,
∵OC是∠AOD的平分线,
∴∠AOC=$\frac{1}{2}$∠AOD=50°.
点评 本题考查了角平分线定义,邻补角定义,掌握角平分线把已知角分成两个相等的角是解题的关键.

练习册系列答案
相关题目
10.已知a-2b=3,则8-a+2b的值是( )
| A. | 3 | B. | 5 | C. | -3 | D. | -5 |
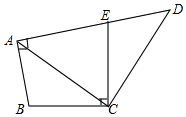 如图,在四边形ABCD中,点E在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.求证:AD=AE+AB.
如图,在四边形ABCD中,点E在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.求证:AD=AE+AB.