题目内容
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于C点,图中的虚线表示该抛物线的对称轴,连接AC与BC.
(1)求该函数的解析式?
(2)求△ABC的面积?
(3)抛物线上是否存在一点Q使得S△ABQ:S△ABC=4:3?若存在Q点,请求出Q点坐标;若不存在,请说明理由.(注意:S△ABQ:表示△ABQ的面积)

(1)求该函数的解析式?
(2)求△ABC的面积?
(3)抛物线上是否存在一点Q使得S△ABQ:S△ABC=4:3?若存在Q点,请求出Q点坐标;若不存在,请说明理由.(注意:S△ABQ:表示△ABQ的面积)

考点:二次函数综合题
专题:
分析:(1)把A(-1,0),B(3,0),C(0,-1)代入抛物线y=ax2+bx+c,即可得出抛物线的解析式.
(2)由AB=4,OC=1,根据三角形的面积公式求解即可,
(3)利用比例式求出S△ABQ,利用三角形的面积公式求出|Q纵坐标|,再分两种情况求解即可.
(2)由AB=4,OC=1,根据三角形的面积公式求解即可,
(3)利用比例式求出S△ABQ,利用三角形的面积公式求出|Q纵坐标|,再分两种情况求解即可.
解答:解:(1)∵A(-1,0),B(3,0),C(0,-1),
∴代入抛物线y=ax2+bx+c得
,
解得
.
∴抛物线的解析式为y=
x2-
x-1.
(2)∵AB=4,OC=1,
∴S△ABC=
AB•OC=
×4×1=2.
(3)存在.
理由如下:
∵S△ABQ:S△ABC=4:3,S△ABC=2
∴S△ABQ=
,
∴
×4×|Q纵坐标|=
,解得|Q纵坐标|=
,
①当Q纵坐标=
时,代入y=
x2-
x-1.
=
x2-
x-1.解得x=1±2
,
所以Q1(1+2
,
),Q2(1-2
,
),
②当Q纵坐标=-
时,代入y=
x2-
x-1.
-
=
x2-
x-1.解得x=1,
所以Q3(1,
).
综上所述:Q1(1+2
,
),Q2(1-2
,
),Q3(1,
).
∴代入抛物线y=ax2+bx+c得
|
解得
|
∴抛物线的解析式为y=
| 1 |
| 3 |
| 2 |
| 3 |
(2)∵AB=4,OC=1,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)存在.
理由如下:
∵S△ABQ:S△ABC=4:3,S△ABC=2
∴S△ABQ=
| 8 |
| 3 |
∴
| 1 |
| 2 |
| 8 |
| 3 |
| 4 |
| 3 |
①当Q纵坐标=
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
所以Q1(1+2
| 2 |
| 4 |
| 3 |
| 2 |
| 4 |
| 3 |
②当Q纵坐标=-
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
-
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
所以Q3(1,
| 4 |
| 3 |
综上所述:Q1(1+2
| 2 |
| 4 |
| 3 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是根据Q纵坐标分两种情况讨论求解.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
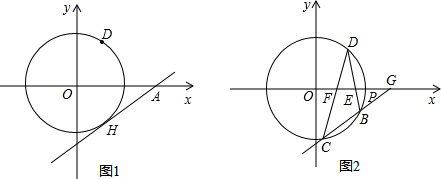
 如图8,点C、D在BE上,BC=DE,∠1=∠2,要使得△ABD≌△AEC,还需要添加一个条件,你添加的条件是
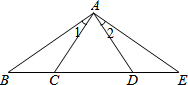
如图8,点C、D在BE上,BC=DE,∠1=∠2,要使得△ABD≌△AEC,还需要添加一个条件,你添加的条件是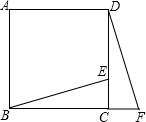 如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF,BE与DF之间有怎样的关系?说明理由.
如图,在正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF,BE与DF之间有怎样的关系?说明理由. 如图,AD是△ABC的BC边上的中线,AB=7,AD=5,则AC的取值范围为
如图,AD是△ABC的BC边上的中线,AB=7,AD=5,则AC的取值范围为