题目内容
已知⊙O过点D(3,4),点H与点D关于x轴对称,过H作⊙O的切线交x轴于点A.
(1)求sin∠HAO的值;
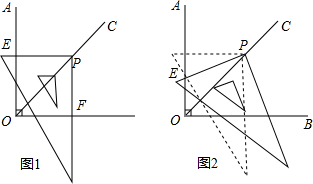
(2)如图2,设⊙O与x轴正半轴交点为P,点E、F是线段OP上的动点(与点P不重合),连接并延长DE、DF交⊙O于点B、C,直线BC交x轴于点G,若△DEF是以EF为底的等腰三角形,求sin∠CGO的值.
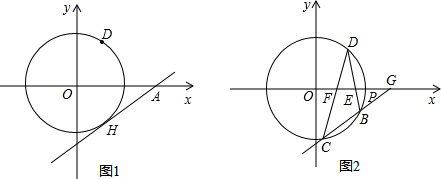
(1)求sin∠HAO的值;
(2)如图2,设⊙O与x轴正半轴交点为P,点E、F是线段OP上的动点(与点P不重合),连接并延长DE、DF交⊙O于点B、C,直线BC交x轴于点G,若△DEF是以EF为底的等腰三角形,求sin∠CGO的值.
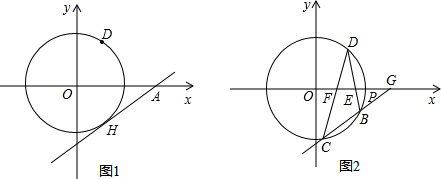
考点:圆的综合题
专题:综合题
分析:(1)连接OH,DH,DH交x轴于Q,如图1,利用关于x轴的点的坐标特征得到H(3,-4),再根据切线的性质,由AH与⊙O相切于H得到OH⊥AH,则可利用等角的余角相等得到∠HAO=∠QHO;在Rt△OQH中,根据勾股定理计算出OH=5,然后根据正弦的定义计算出sin∠QHO=
,即有sin∠HAO=
;
(2)作DH⊥x轴于H,交⊙O于M,连接OM交BC于N,如图,由OH⊥DM,根据垂径定理得HD=HM,则点M与点D关于x轴对称,则M(3,-4),再根据等腰三角形的性质得DH平分∠FDE,即∠CDM=∠BDM,则根据圆周角定理得到
=
,接着可利用垂径定理的推论得到OM⊥BC,则∠NGO+∠NOG=90°,利用等角的余角相等得到∠NGO=∠OMH,在Rt△OMH中,用勾股定理计算出OM=5,于是可根据正弦的定义得到sin∠OMH=
,则sin∠NGO=
,即sin∠CGO=
.
| 3 |
| 5 |
| 3 |
| 5 |
(2)作DH⊥x轴于H,交⊙O于M,连接OM交BC于N,如图,由OH⊥DM,根据垂径定理得HD=HM,则点M与点D关于x轴对称,则M(3,-4),再根据等腰三角形的性质得DH平分∠FDE,即∠CDM=∠BDM,则根据圆周角定理得到
 |
| CM |
 |
| BM |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
解答:解:(1)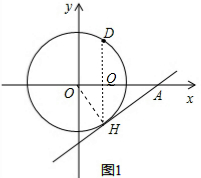 连接OH,DH,DH交x轴于Q,如图1,
连接OH,DH,DH交x轴于Q,如图1,
∵点H与点D关于x轴对称,
∴x轴垂直平分DH,
而D(3,4),
∴H(3,-4),
∵AH与⊙O相切于H,
∴OH⊥AH,
∴∠HAO+∠AOH=90°,
而∠QHO+∠AOH=90°,
∴∠HAO=∠QHO,
在Rt△OQH中,∵OQ=3,QH=4,
∴OH=
=5,
∴sin∠QHO=
=
,
∴sin∠HAO=
;
(2)作DH⊥x轴于H,交⊙O于M,连接OM交BC于N,如图2,
∵OH⊥DM,
∴HD=HM,
∴点M与点D关于x轴对称,
而D(3,4),
∴M(3,-4),
∵△DEF是以EF为底的等腰三角形,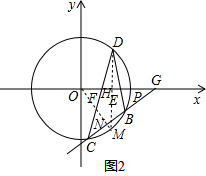
∴DH平分∠FDE,即∠CDM=∠BDM,
∴
=
,
∴OM⊥BC,
∴∠ONG=90°,
∴∠NGO+∠NOG=90°,
而∠NOG+∠OMH=90°,
∴∠NGO=∠OMH,
在Rt△OMH中,∵OH=3,MH=4,
∴OM=
=5,
∴sin∠OMH=
=
,
∴sin∠NGO=
,
即sin∠CGO=
.
 连接OH,DH,DH交x轴于Q,如图1,
连接OH,DH,DH交x轴于Q,如图1,∵点H与点D关于x轴对称,
∴x轴垂直平分DH,
而D(3,4),
∴H(3,-4),
∵AH与⊙O相切于H,
∴OH⊥AH,
∴∠HAO+∠AOH=90°,
而∠QHO+∠AOH=90°,
∴∠HAO=∠QHO,
在Rt△OQH中,∵OQ=3,QH=4,
∴OH=
| OQ2+QH2 |
∴sin∠QHO=
| OQ |
| OH |
| 3 |
| 5 |
∴sin∠HAO=
| 3 |
| 5 |
(2)作DH⊥x轴于H,交⊙O于M,连接OM交BC于N,如图2,
∵OH⊥DM,
∴HD=HM,
∴点M与点D关于x轴对称,
而D(3,4),
∴M(3,-4),
∵△DEF是以EF为底的等腰三角形,

∴DH平分∠FDE,即∠CDM=∠BDM,
∴
 |
| CM |
 |
| BM |
∴OM⊥BC,
∴∠ONG=90°,
∴∠NGO+∠NOG=90°,
而∠NOG+∠OMH=90°,
∴∠NGO=∠OMH,
在Rt△OMH中,∵OH=3,MH=4,
∴OM=
| OH2+MH2 |
∴sin∠OMH=
| OH |
| OM |
| 3 |
| 5 |
∴sin∠NGO=
| 3 |
| 5 |
即sin∠CGO=
| 3 |
| 5 |
点评:本题考查了圆的综合题:熟练掌握垂径定理及其推论、圆周角定理和切线的性质;会运用勾股定理和锐角三角函数的定义进行几何计算;理解关于x轴对称的点的坐标特征和坐标与图形性质.

练习册系列答案
相关题目
 已知,如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,周长记作C1;再作第二个正方形A2B2C2A3,周长记作C2;继续作第三个正方形A3B3C3A4,周长记作C3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Cn=
已知,如图,∠MON=45°,OA1=1,作正方形A1B1C1A2,周长记作C1;再作第二个正方形A2B2C2A3,周长记作C2;继续作第三个正方形A3B3C3A4,周长记作C3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Cn= 如图,抛物线y=
如图,抛物线y=