题目内容
如图，AD是△ABC的BC边上的中线，AB=7，AD=5，则AC的取值范围为考点：全等三角形的判定与性质,三角形三边关系
专题：
分析：延长AD至E，使DE=AD，连接CE．根据SAS证明△ABD≌△ECD，得CE=AB，再根据三角形的三边关系即可求解．
解答：
解：延长AD至E，使DE=AD=5，连接CE．
在△ABD和△ECD中，
，
∴△ABD≌△ECD，
∴CE=AB．
在△ACE中，AE-EC＜AC＜AE+CE，
即5+5-7＜AC＜5+5+7，
3＜AC＜17．
故答案为3＜AC＜17．
解：延长AD至E，使DE=AD=5，连接CE．在△ABD和△ECD中，
|
∴△ABD≌△ECD，
∴CE=AB．
在△ACE中，AE-EC＜AC＜AE+CE，
即5+5-7＜AC＜5+5+7，
3＜AC＜17．
故答案为3＜AC＜17．
点评：此题综合运用了全等三角形的判定和性质、三角形的三边关系．注意：倍长中线是常见的辅助线之一．
练习册系列答案
阅读快车系列答案
相关题目
如图，某农场有一堵墙AD长35m，现用59m长的篱笆围起一个养鸡场，并留有1m宽的门，当养鸡场的长BC为多少时，所围矩形养鸡场的面积最大？
如图，在△ABC中，将边AB绕点B旋转60°至DB，将边AC绕点C旋转60°至EC，连结DA、EA、DC、EB，BE与CD相交于F，则下列结论不正确的是（ ）| A、△ABD是等边三角形 |
| B、△ACE是等边三角形 |
| C、AF平分∠DFE |
| D、点F平分BE |
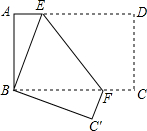如图，将长方形纸片ABCD折叠，使点D与点B重合，点C落在点C′出，折痕为EF，