题目内容
若x+y+z=0,则x(
+
)+y(
+
)+z(
+
)的值是 .
| 1 |
| y |
| 1 |
| z |
| 1 |
| x |
| 1 |
| z |
| 1 |
| x |
| 1 |
| y |
考点:分式的化简求值
专题:
分析:先根据分式混合运算的法则把原式进行化简,再把x+y+z=0代入进行计算即可.
解答:解:原式=
+
+
+
+
+
=
+
+
∵x+y+z=0,
∴x=-(y+z),y=-(x+z),z=-(x+y),
∴原式=
+
+
=-1-1-1
=-3.
故答案为:-3.
| x |
| y |
| x |
| z |
| y |
| x |
| y |
| z |
| z |
| x |
| z |
| y |
=
| x+y |
| z |
| x+z |
| y |
| z+y |
| x |
∵x+y+z=0,
∴x=-(y+z),y=-(x+z),z=-(x+y),
∴原式=
| x+y |
| -(x+y) |
| x+z |
| -(x+z) |
| x+y |
| -(x+y) |
=-1-1-1
=-3.
故答案为:-3.
点评:本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
(-12)÷〔(-3)+(-15)〕÷(+5)=( )
A、
| ||
B、-
| ||
C、-
| ||
D、
|
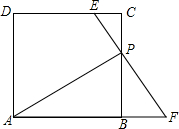 如图,在正方形ABCD中,点P从C点出发,沿射线CB运动,连接AP,过点P作EP⊥AP,分别交直线CD、AB的延长线于点E、F.
如图,在正方形ABCD中,点P从C点出发,沿射线CB运动,连接AP,过点P作EP⊥AP,分别交直线CD、AB的延长线于点E、F.