题目内容
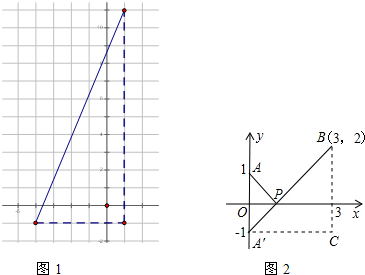
1.问题情境:在平面直角坐标系中,已知A(-4,-1)、B(1.11),如果要求A、B两点之间的距离,可以构造如图1所示的直角三角形,则A、B两点之间的距离为13.
结论:在平面直角坐标系中,已知平面内A(x1,y1)、B(x2,y2)两点坐标,则A、B两点之间的距离等于$\sqrt{({x}_{2}-{x}_{1})^{2}+({y}_{2}-{y}_{1})^{2}}$.
探究1:求代数式$\sqrt{{x}^{2}+1}+\sqrt{(x-3)^{2}+4}$的最小值.
解:$\sqrt{{x}^{2}+1}+\sqrt{(x-3)^{2}+4}$=$\sqrt{(x-0)^{2}+(0-1)^{2}}+\sqrt{(x-3)^{2}+(0-2)^{2}}$
如图2,建立平面直角坐标系,点P(x,0)是x轴上一点,
则$\sqrt{(x-0)^{2}+(0-1)^{2}}$可以看成点P(x,0)与点A(0,1)的距离
$\sqrt{(x-3)^{2}+(0-2)^{2}}$可以看成点P(x,0)与点B(3,2)的距离,
所以原代数式的值可以看成线段PA与PB的长度之和,PA+PB的最小值就是原代数式的最小值.
设点A关于x轴的对称点为A′,则PA=PA′,因此,求PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B之间的所有连线中线段最短,所以PA′+PB的最小值为线段A′B的长度.为此,构造直角三角形A′CB,因为A′C=3,CB=3,所以A′B=$3\sqrt{2}$
,即$\sqrt{{x}^{2}+1}+\sqrt{(x-3)^{2}+4}$的最小值为$3\sqrt{2}$.
探究2:求代数式$\sqrt{(x-2)^{2}+1}+\sqrt{(x-4)^{2}+9}$的最小值.
解:$\sqrt{(x-2)^{2}+1}+\sqrt{(x-4)^{2}}+9$的值可以看成平面直角坐标系中点P(x,0)与点A(2,1)、点B(4,3)的距离之和,$\sqrt{(x-2)^{2}+1}+\sqrt{(x-4)^{2}+9}$ 的最小值为2$\sqrt{5}$.
探究3:代数式$\sqrt{{x}^{2}+25}+\sqrt{{x}^{2}-4x+5}$的最小值为2$\sqrt{10}$.
分析 如图1,利用勾股定理计算A、B两点之间的距离;
对于探究2,由于$\sqrt{(x-2)^{2}+1}+\sqrt{(x-4)^{2}+9}$=$\sqrt{(x-2)^{2}+(0-1)^{2}}$+$\sqrt{(x-4)^{2}+(0-3)^{2}}$,则$\sqrt{(x-2)^{2}+1}+\sqrt{(x-4)^{2}+9}$的值可以看成平面直角坐标系中点P(x,0)与点A(2,1)、点B(4,3)的距离之和,利用探究1的方法,求出点A(2,1)关于x轴的对称点为A′(2,-1),再利用两点间的距离公式计算出BA′=2$\sqrt{5}$,则得到$\sqrt{(x-2)^{2}+1}+\sqrt{(x-4)^{2}+9}$ 的最小值为2$\sqrt{5}$;
对于探究3,先变形得到$\sqrt{{x}^{2}+25}+\sqrt{{x}^{2}-4x+5}$=$\sqrt{(x-0)^{2}+(0-5)^{2}}$+$\sqrt{(x-2)^{2}+(0-1)^{2}}$,然后根据探究1的方法求解.
解答 解:如图1,A、B两点之间的距离=$\sqrt{(1+4)^{2}+(11+1)^{2}}$=13;
探究2:求代数式$\sqrt{(x-2)^{2}+1}+\sqrt{(x-4)^{2}+9}$的最小值.
解:$\sqrt{(x-2)^{2}+1}+\sqrt{(x-4)^{2}+9}$=$\sqrt{(x-2)^{2}+(0-1)^{2}}$+$\sqrt{(x-4)^{2}+(0-3)^{2}}$,
所以$\sqrt{(x-2)^{2}+1}+\sqrt{(x-4)^{2}+9}$的值可以看成平面直角坐标系中点P(x,0)与点A(2,1)、点B(4,3)的距离之和,
点A(2,1)关于x轴的对称点为A′(2,-1),则BA′=$\sqrt{(4-2)^{2}+(3+1)^{2}}$=2$\sqrt{5}$,
所以$\sqrt{(x-2)^{2}+1}+\sqrt{(x-4)^{2}+9}$ 的最小值为2$\sqrt{5}$;
探究3:$\sqrt{{x}^{2}+25}+\sqrt{{x}^{2}-4x+5}$=$\sqrt{(x-0)^{2}+(0-5)^{2}}$+$\sqrt{(x-2)^{2}+(0-1)^{2}}$,
所以$\sqrt{{x}^{2}+25}+\sqrt{{x}^{2}-4x+5}$的值可以看成平面直角坐标系中点P(x,0)与点A(0,5)、点B(2,1)的距离之和,
而点A(0,5)关于x轴的对称点为A′(0,-5),则BA′=$\sqrt{(2-0)^{2}+(1+5)^{2}}$=2$\sqrt{10}$.
故答案为13;2,1,4,3;2$\sqrt{5}$;2$\sqrt{10}$.
点评 本题考查了轴对称-最短路线问题:在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L的交点就是所要找的点.也考查了坐标与图形性质.

 快捷英语周周练系列答案
快捷英语周周练系列答案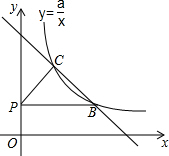 如图,在平面直角坐标系中,动点P从原点O开始沿y轴的正方向运动,点B、C是一次 函数y=kx+b与反比例函数y=$\frac{a}{x}$(a>0,x>0)的图象的两个交点,且点B(m,2).当点P的坐标为(0,2)时,PC=BC,且∠PCB=90°.
如图,在平面直角坐标系中,动点P从原点O开始沿y轴的正方向运动,点B、C是一次 函数y=kx+b与反比例函数y=$\frac{a}{x}$(a>0,x>0)的图象的两个交点,且点B(m,2).当点P的坐标为(0,2)时,PC=BC,且∠PCB=90°. 如图,直线a、b相交于点O,∠1=50°,则∠2=50度.
如图,直线a、b相交于点O,∠1=50°,则∠2=50度.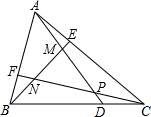 如图,在面积为1的△ABC中,点D,E,F分别在边BC,CA,AB上,且$\frac{BD}{DC}$=$\frac{CE}{EA}$=$\frac{AF}{FB}$=k>1,连接AD,BE,CF,得△PMN,则△PMN的面积为$\frac{{k}^{2}-2k+1}{{k}^{2}+k+1}$.
如图,在面积为1的△ABC中,点D,E,F分别在边BC,CA,AB上,且$\frac{BD}{DC}$=$\frac{CE}{EA}$=$\frac{AF}{FB}$=k>1,连接AD,BE,CF,得△PMN,则△PMN的面积为$\frac{{k}^{2}-2k+1}{{k}^{2}+k+1}$.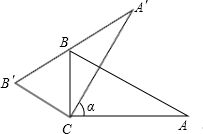 直角三角板ABC中,∠A=30°,BC=2.将其绕直角顶点C逆时针旋转一个角α(0°<α<120°且α≠90°),得到Rt△A′B′C′
直角三角板ABC中,∠A=30°,BC=2.将其绕直角顶点C逆时针旋转一个角α(0°<α<120°且α≠90°),得到Rt△A′B′C′