题目内容
16.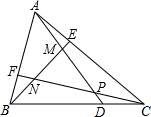 如图,在面积为1的△ABC中,点D,E,F分别在边BC,CA,AB上,且$\frac{BD}{DC}$=$\frac{CE}{EA}$=$\frac{AF}{FB}$=k>1,连接AD,BE,CF,得△PMN,则△PMN的面积为$\frac{{k}^{2}-2k+1}{{k}^{2}+k+1}$.
如图,在面积为1的△ABC中,点D,E,F分别在边BC,CA,AB上,且$\frac{BD}{DC}$=$\frac{CE}{EA}$=$\frac{AF}{FB}$=k>1,连接AD,BE,CF,得△PMN,则△PMN的面积为$\frac{{k}^{2}-2k+1}{{k}^{2}+k+1}$.
分析 设S△FBN=a,则S△FNA=ka,设S△ANE=b,则S△CNE=kb,由$\frac{AF}{AB}$=$\frac{k}{k+1}$,△ABC的面积为1,求得S△AFC=$\frac{k}{k+1}$,同理S△AEB=$\frac{1}{k+1}$,列出方程组解出a,b的值,同理S△CDP=S△AEM=a,S△ADC=S△BCF=$\frac{1}{k+1}$,由S△PMN=1-$\frac{3}{k+1}$+3a即可得出△PMN的面积.
解答 解:如图,设S△FBN=a,则S△FNA=ka,
设S△ANE=b,则S△CNE=kb,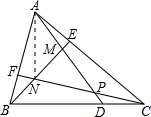
∵$\frac{AF}{AB}$=$\frac{k}{k+1}$,△ABC的面积为1,
∴S△AFC=$\frac{k}{k+1}$,同理S△AEB=$\frac{1}{k+1}$,
即$\left\{\begin{array}{l}{ka+b+kb=\frac{k}{k+1}}\\{a+ka+b=\frac{1}{k+1}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{(k+1)({k}^{2}+k+1)}}\\{b=\frac{{k}^{2}}{(k+1)({k}^{2}+k+1)}}\end{array}\right.$,
同理S△CDP=S△AEM=a,S△ADC=S△BCF=$\frac{1}{k+1}$,
∴S△PMN=1-$\frac{3}{k+1}$+3a=1-$\frac{3}{k+1}$+$\frac{3}{(k+1)({k}^{2}+k+1)}$=$\frac{{k}^{2}-2k+1}{{k}^{2}+k+1}$.
故答案为:$\frac{{k}^{2}-2k+1}{{k}^{2}+k+1}$.
点评 本题主要考查了面积及等积变换,解题的关键是求出S△FBN=S△CDP=S△AEM及S△AEB=S△ADC=S△BCF.

 全优点练单元计划系列答案
全优点练单元计划系列答案 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )| A. | 2.5 | B. | 2.8 | C. | 3 | D. | 3.2 |
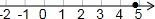

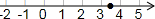
 有理数a,b,c在数轴上对应的点如:用“>”或“<”号填空
有理数a,b,c在数轴上对应的点如:用“>”或“<”号填空 已知线段AB=a,在线段AB上有一点C,若AC=$\frac{3-\sqrt{5}}{2}$a,则点C是线段AB的黄金分割点吗?为什么?
已知线段AB=a,在线段AB上有一点C,若AC=$\frac{3-\sqrt{5}}{2}$a,则点C是线段AB的黄金分割点吗?为什么?
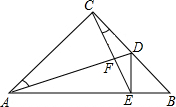 如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD是BC上的中线,CE⊥AD于F,交AB于E,连结DE,问∠CDA与∠BDE相等吗?为什么?
如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD是BC上的中线,CE⊥AD于F,交AB于E,连结DE,问∠CDA与∠BDE相等吗?为什么?