题目内容
12. 如图,直线a、b相交于点O,∠1=50°,则∠2=50度.
如图,直线a、b相交于点O,∠1=50°,则∠2=50度.
分析 根据对顶角相等和已知得到答案.
解答 解:根据对顶角相等可知,
∠2=∠1=50°,
故答案为:50°.
点评 本题考查的是对顶角的概念和性质,认识对顶角、掌握对顶角相等是解题的关键》

练习册系列答案
相关题目
7. 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )| A. | 2.5 | B. | 2.8 | C. | 3 | D. | 3.2 |
2.在实数-4、0、2、5中,最小的实数是( )
| A. | -4 | B. | 0 | C. | 2 | D. | 5 |
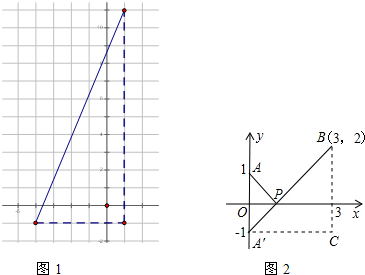
 如图,线段AB=10,点P是AB的动点,分别以AP、BP为边在线段AB的同侧作正方形APMN、PBEF,连结ME,则ME的最小值是2$\sqrt{5}$.
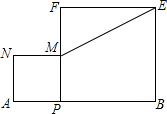
如图,线段AB=10,点P是AB的动点,分别以AP、BP为边在线段AB的同侧作正方形APMN、PBEF,连结ME,则ME的最小值是2$\sqrt{5}$. 如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连结CF.
如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连结CF.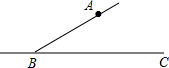 利用尺规作图(保留作图痕迹即可):如图,在射线BC上,作线段BD,使BD=2AB;以点D为顶点,射线DC为一边,作∠EDC(两种情况),使∠EDC=∠ABC.
利用尺规作图(保留作图痕迹即可):如图,在射线BC上,作线段BD,使BD=2AB;以点D为顶点,射线DC为一边,作∠EDC(两种情况),使∠EDC=∠ABC. 有理数a,b,c在数轴上对应的点如:用“>”或“<”号填空
有理数a,b,c在数轴上对应的点如:用“>”或“<”号填空