题目内容
13.如图1,等边△ABC的边长为4cm,动点D从点B出发,沿射线BC方向移动,以AD为边作等边△ADE.(1)在点D运动的过程中,点E能否移动至直线AB上?若能,求出此时BD的长;若不能,请说明理由;
(2)如图2,在点D从点B开始移动至点C的过程中,以等边△ADE的边AD、DE为边作?ADEF.
①?ADEF的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
②若点M、N、P分别为AE、AD、DE上动点,直接写出MN+MP的最小值.
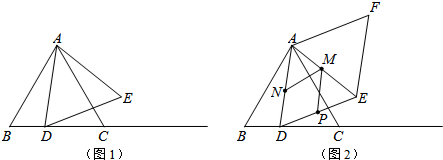
分析 (1)根据等边三角形的性质可知:∠BAC=∠ACB=∠EAD=60°,由三角形外角的性质可知∠ACB=∠CAD+∠ADC=60°,从而可知:∠CAD<60°,所以∠CAD+∠BAC+∠EAD<180°,故此点E不能移动到直线AB上;
(2)因为△ADE的面积=$\frac{1}{2}$AD•ADsin60°,所以当AD最短时,△ADE的面积有最小,根据垂线段最短可知当AD⊥BC时,△ADE的面积有最小值,四边形ADEF为平四边形,AE为对角线,所以平行四边形ADEF的面积是△ADE面积的2倍,所以三角形ADE的面积最小时,平行四边形的面积最小;
(3)当点N、M、P在一条直线上,且NP⊥AD时,MN+MP有最小值,最小值为AD与EF之间的距离.
解答 解:(1)不存在.
理由:如图1所示:
∵△ABC和△ADE均为等边三角形,
∴∠BAC=∠ACB=∠EAD=60°.
∵∠ACB=∠CAD+∠ADC=60°,
∴∠CAD<60°,
又∵∠BAC=∠EAD=60°,
∴∠CAD+∠BAC+∠EAD<180°.
∴点E不能移动到直线AB上.
(2)①存在:在图(2)中,当AD⊥BC时△ADE的面积最小.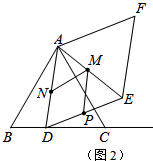
在Rt△ADB中,AD=ABsin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$.
∴△ADE的面积=$\frac{1}{2}$AD•ADsin60°=$\frac{1}{2}$×2$\sqrt{3}$×2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∵四边形ADEF为平四边形,AE为对角线,
∴平行四边形ADEF的面积是△ADE面积的2倍.
∴?ADEF的面积的最小值=2×3$\sqrt{3}$=6$\sqrt{3}$;
②如图3所示:作点P关于AE的对称点P1,
当点N、M、P在一条直线上,且NP⊥AD时,MN+MP有最小值,
过点A作AG∥NP1,
∵AN∥GP1,AG∥NP1,
∴四边形ANP1G为平行四边形.
∴NP1=AG=AF•sin60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3.
即MN+MP的最小值为3
点评 本题主要考查的是等边三角形的性质,特殊锐角三角函数,平行四边形的性质以及最短路径等知识点,明确?ADEF的面积最小和MN+MP有最小值时的条件时解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | -4 | B. | 0 | C. | 2 | D. | 5 |
 如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连结CF.
如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连结CF. 有理数a,b,c在数轴上对应的点如:用“>”或“<”号填空
有理数a,b,c在数轴上对应的点如:用“>”或“<”号填空
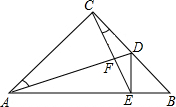 如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD是BC上的中线,CE⊥AD于F,交AB于E,连结DE,问∠CDA与∠BDE相等吗?为什么?
如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD是BC上的中线,CE⊥AD于F,交AB于E,连结DE,问∠CDA与∠BDE相等吗?为什么?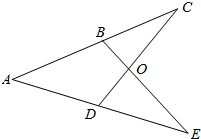 如图,已知B、D分别是AC、AE的中点,且AB=AD,OD=OB,求证:OE=OC.
如图,已知B、D分别是AC、AE的中点,且AB=AD,OD=OB,求证:OE=OC.
