题目内容
1.求一次函数y=3x-2与x轴的交点坐标($\frac{2}{3}$,0),与y轴的交点坐标(0,-2),直线与两坐标轴所围成的三角形面积为$\frac{2}{3}$.分析 分别求得函数y=3x-2与x轴、y轴的交点坐标,那么这条直线与两坐标轴围成的三角形的面积等于x轴,y轴上的数的积的绝对值的一半,把相关数值代入求解即可.
解答 解:当x=0时,y=-2,
当y=0时,x=$\frac{2}{3}$,
∴这条直线与两坐标轴围成的三角形的面积为$\frac{1}{2}$×|-2×$\frac{2}{3}$|=$\frac{2}{3}$,
故答案为:($\frac{2}{3}$,0),(0,-2),$\frac{2}{3}$
点评 考查一次函数图象上的点的坐标的特点;用到的知识点为:x轴上的点的纵坐标为0;y轴上的点的横坐标为0.

练习册系列答案
相关题目
13. 如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )
如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )
 如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )
如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )| A. | $\frac{BC}{AC}$=$\frac{\sqrt{5}-1}{2}$ | B. | AC+BC=$\frac{\sqrt{5}-1}{2}$AB | C. | $\frac{AC}{AB}$=$\frac{\sqrt{5}-1}{2}$ | D. | AC2=AB•BC |
10.图中是正方体的平面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
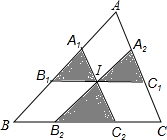 如图,△ABC的内切⊙I的半径为4cm,线段B1C1,A1C2、A2B2都经过内心I,并且分别与△ABC的边平行,己知IA1+IB2+IC1=5,△ABC的面积为32m2,则图中阴影部分的面积为( )
如图,△ABC的内切⊙I的半径为4cm,线段B1C1,A1C2、A2B2都经过内心I,并且分别与△ABC的边平行,己知IA1+IB2+IC1=5,△ABC的面积为32m2,则图中阴影部分的面积为( )