题目内容
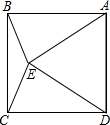 如图,在正方形ABCD的内部作等边△ADE,连接BE、CE,求∠BEC的度数.
如图,在正方形ABCD的内部作等边△ADE,连接BE、CE,求∠BEC的度数.考点:正方形的性质,等腰三角形的性质,等边三角形的性质
专题:几何图形问题
分析:根据等边三角形的性质可得AD=DE,根据正方形的性质可得AD=DC,从而得到DE=DC,再根据等边对等角可得∠CED=∠ECD,然后求出∠CDE=30°,再求出∠CED,再根据对称性利用周角等于360°列式计算即可得解.
解答:解:∵△ADE是等边三角形,
∴AD=DE,
∵四边形ABCD是正方形,
∴AD=DC,
∴DE=DC,
∴∠CED=∠ECD,
∴∠CDE=∠ADC-∠ADE=90°-60°=30°,
∴∠CED=∠ECD=
(180°-30°)=75°,
∴∠BEC=360°-75°×2-60°=150°.
∴AD=DE,
∵四边形ABCD是正方形,
∴AD=DC,
∴DE=DC,
∴∠CED=∠ECD,
∴∠CDE=∠ADC-∠ADE=90°-60°=30°,
∴∠CED=∠ECD=
| 1 |
| 2 |
∴∠BEC=360°-75°×2-60°=150°.
点评:本题考查了正方形的性质,等边三角形的性质,等腰三角形的判定与性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
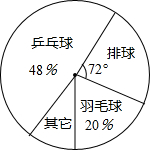 某班60名学生喜欢各类体育活动,他们最喜欢的一项体育活动情况见扇形统计图,现给出以下说法
某班60名学生喜欢各类体育活动,他们最喜欢的一项体育活动情况见扇形统计图,现给出以下说法①最受欢迎的球类运动是乒乓球;
②最喜欢排球的学生达到班级学生总数的
| 1 |
| 5 |
③最喜欢羽毛球的学生达到班级学生总数的12人.
④最喜欢其他运动的学生达到12%
其中正确的结论为( )
| A、①②③ | B、①③④ |
| C、①②④ | D、①②③④ |
在四边形中,能判定这个四边形是正方形的条件是( )
| A、对角线相等,对边平行且相等 |
| B、一组对边平行,一组对角相等 |
| C、对角线互相平分且相等,对角线互相垂直 |
| D、一组邻边相等,对角线互相平分 |
反比例函数y=-
与正比例函数y=kx的一个交点为(-1,2),则关于x的方程-
=kx的解为( )
| 2 |
| x |
| 2 |
| x |
| A、x1=-1,x2=1 |
| B、x1=-1,x2=2 |
| C、x1=-2,x2=1 |
| D、x1=-1,x2=-2 |
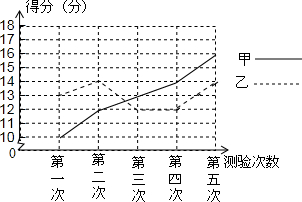 甲乙两人参加某体育项目训练,近期的五次测验得分情况(单位:分)如图所示
甲乙两人参加某体育项目训练,近期的五次测验得分情况(单位:分)如图所示