题目内容
有一个三位数,其各数位的数字和是16,十位数字是个位数字和百位数字的和,如果把百位数字与个位数字对调,那么新数比原数大594,求原数.(用一元一次的方法解答)
考点:一元一次方程的应用
专题:
分析:设这个三位数的百位数字为a,十位数字为b,个位数字为c,根据各数位的数字和是16,十位数字是个位数字和百位数字的和,得出a+b+c=16和b=a+c,求出b和a+c的值,再根据百位数字与个位数字对调,得出新数比原数大594,得出100c+10b+a-100a-10b-c=594,求出a,c的值,即可得出原数.
解答:解:设这个三位数的百位数字为a,十位数字为b,个位数字为c,根据题意得;
a+b+c=16①,
b=a+c②,
100c+10b+a-100a-10b-c=594③,
由①和②求得b=8,a+c=8,
将a=8-c代入③求得c=7,a=1,
则原数是187.
a+b+c=16①,
b=a+c②,
100c+10b+a-100a-10b-c=594③,
由①和②求得b=8,a+c=8,
将a=8-c代入③求得c=7,a=1,
则原数是187.
点评:此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
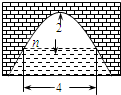 如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加( )
如图是抛物线形拱桥,当拱顶离水面2m时,水面宽4m,则水面下降1m时,水面宽度增加( )| A、1m | ||
| B、2m | ||
C、(2
| ||
D、(
|
某大米包装袋上标注着“净含量10㎏±150g”,小华从商店买了2袋大米,这两袋大米相差的克数不可能是( )
| A、100g | B、150g |
| C、300g | D、400g |
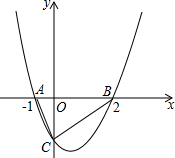 如图:抛物线与x轴交于点A(-1,0),B(2,0).与y轴的负半轴交于点C,且△ABC的面积为3
如图:抛物线与x轴交于点A(-1,0),B(2,0).与y轴的负半轴交于点C,且△ABC的面积为3 一个扇形如图,半径为10cm,圆心角为270°,用它做成一个圆锥的侧面,求圆锥的侧面积.
一个扇形如图,半径为10cm,圆心角为270°,用它做成一个圆锥的侧面,求圆锥的侧面积. 如图,已知在圆内接四边形ABCD中,∠CAD=∠CAB=60°,求证:△BDC是等边三角形.
如图,已知在圆内接四边形ABCD中,∠CAD=∠CAB=60°,求证:△BDC是等边三角形.