题目内容
18.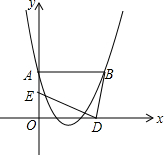 抛物线y=x2+bx+c经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
抛物线y=x2+bx+c经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.(1)求抛物线与x轴的交点坐标;
(2)若点C为抛物线与x轴的交点,是否存在点D,使A、B、C、D四点围成的四边形是平行四边形?若存在,求点D的坐标;若不存在,说明理由;
(3)问几秒钟时,B、D、E在同一条直线上?
分析 (1)把A(0,2),B(3,2)两点代入抛物线y=x2+bx+c即可得到结果;
(2)存在,由已知条件得AB∥x轴,根据平行四边形的性质对边相等列方程即可求得结果;
(3)设t秒钟时,B、D、E在同一条直线上,则OE=t,OD=2t,设直线BD的解析式为:y=kx+b,把B,D,E三点代入,解方程组即可得到答案.
解答 解:(1)抛物线y=x2+bx+c经过A(0,2),B(3,2)两点,
∴$\left\{\begin{array}{l}{2=c}\\{2=9+3b+c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-3}\\{c=2}\end{array}\right.$,
∴抛物线的解析式为:y=x2-3x+2,
令y=0,则x2-3x+2=0,
解得:x1=1,x2=2,
∴抛物线与x轴的交点坐标是(1,0),(2,0);
(2)存在,由已知条件得AB∥x轴,
∴AB∥CD,
∴当AB=CD时,
以A、B、C、D四点围成的四边形是平行四边形,
设D(m,0),
当C(1,0)时,则CD=m-1,
∴m-1=3,
∴m=4,
当C(2,0)时,则CD=m-2,
∴m-2=3,
∴m=5,
∴D(5,0),
综上所述:当D(4,0)或(5,0)时,使A、B、C、D四点围成的四边形是平行四边形;
(3)设t秒钟时,B、D、E在同一条直线上,则OE=t,OD=2t,
∴E(0,t),D(2t,0),
设直线BD的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{t=b}\\{2=3k+b}\\{0=2tk+b}\end{array}\right.$,
解得k=-$\frac{1}{2}$或k=$\frac{2}{3}$(不合题意舍去),
∴当k=-$\frac{1}{2}$,t=$\frac{7}{2}$,
∴点D、E运动$\frac{7}{2}$秒钟时,B、D、E在同一条直线上.
点评 本题考查了待定系数法求二次函数的解析式,平行四边形的判定和性质,一次函数图象上点的坐标特征,正确的理解题意,把握数量之间的关系是解题的关键.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案| A. | $\frac{a+b}{a-b}$ | B. | $\frac{b}{a-b}$ | C. | $\frac{a}{a+b}$ | D. | $\frac{b}{a+b}$ |
| A. | x-1 | B. | 2x | C. | 2x+1 | D. | x+1 |
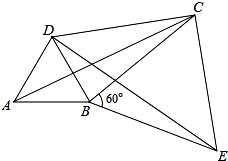 给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.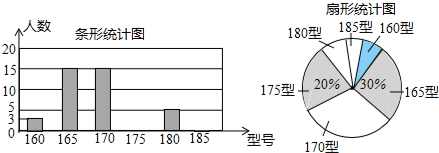
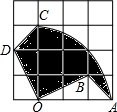 如图,在4×4的正方形网格中,每个小正方形的边长均为1,将△AOB绕点O逆时针旋转90°得到△COD,则旋转过程中形成的阴影部分的面积为$\frac{9}{4}π$.
如图,在4×4的正方形网格中,每个小正方形的边长均为1,将△AOB绕点O逆时针旋转90°得到△COD,则旋转过程中形成的阴影部分的面积为$\frac{9}{4}π$.