题目内容
3. 如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,点P不与O,D重合,连接PA.设∠PAB=β,则β的取值范围是60°<β<75°.
如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,点P不与O,D重合,连接PA.设∠PAB=β,则β的取值范围是60°<β<75°.
分析 当P点与D点重合是∠DAB=75°,与O重合则OAB=60°,∠OAB<∠PAB<∠DAB,即可得出结果.
解答 解:连接DA,OA,则△OAB是等边三角形,
∴∠OAB=∠AOB=60°,
∵DC是直径,DC⊥AB,
∴∠AOC=$\frac{1}{2}$∠AOB=30°,
∴∠ADC=15°,
∴∠DAB=75°,
∵∠OAB<∠PAB<∠DAB,
∴60°<β≤<5°;
故答案为:60°<β<75°.
点评 本题考查了垂径定理,等边三角形的判定及性质,圆周角定理;熟练掌握垂径定理和圆周角定理是解决问题的关键.

练习册系列答案
相关题目
10.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

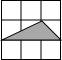
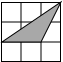
 如图,下列图中小正方形的边长为1,阴影三角形的顶点均在格点上,与△ABC相似的是( )
如图,下列图中小正方形的边长为1,阴影三角形的顶点均在格点上,与△ABC相似的是( )

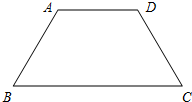 如图,在梯形ABCD中,AD∥BC,若AB=AD=DC=2,∠A=120°,则梯形ABCD的周长为10.
如图,在梯形ABCD中,AD∥BC,若AB=AD=DC=2,∠A=120°,则梯形ABCD的周长为10.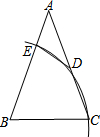 如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,分别交AC、AB于点D、E,连接DE,则∠ADE=36°.
如图,在△ABC中,AB=AC,∠A=36°,以B为圆心,BC为半径作弧,分别交AC、AB于点D、E,连接DE,则∠ADE=36°. 数学活动课上,四位同学围绕作图问题:“如图,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形,其中作法错误的为( )
数学活动课上,四位同学围绕作图问题:“如图,已知直线l和直线l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形,其中作法错误的为( )


