题目内容
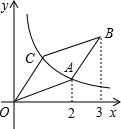 如图,?ABCD的顶点O在原点,顶点A、C在反比例函数y=
如图,?ABCD的顶点O在原点,顶点A、C在反比例函数y=| k |
| x |
考点:平行四边形的性质,反比例函数系数k的几何意义
专题:
分析:首先过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E,作点B作BF⊥x轴,作AF∥x轴,交于点F,连接AC,易求得点C的横坐标为1,又由平行四边形OABC的面积为4,可得S△OAC=S△OCD+S梯形AEDC-S△OAE=S梯形AEDC=
(AE+CD)•DE=2,解此方程即可求得k的值.
| 1 |
| 2 |
解答: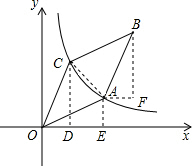 解:过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E,作点B作BF⊥x轴,作AF∥x轴,交于点F,连接AC,
解:过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E,作点B作BF⊥x轴,作AF∥x轴,交于点F,连接AC,
∵四边形OABC是平行四边形,
∴OC=AB,OC∥AB,
∴∠COD=∠BAF,
在△COD和△BAF中,
∵
,
∴△COD≌△BAF(AAS),
∴OD=AF,
∵点A的横坐标为2,点B的横坐标为3,
∴AF=1,
∴OD=1,
即点C的横坐标为1,
∵顶点A,C在反比例函数y=
的图象上,
∴点A(2,
),点C(1,k),S△OCD=S△OAE,
∴DE=OE-OD=4-2=2,
∵平行四边形OABC的面积为4,
∴S△OAC=2,
∴S△OAC=S△OCD+S梯形AEDC-S△OAE=S梯形AEDC=
(AE+CD)•DE=
×(
+k)×1=2,
解得:k=
.
故答案为:
.
 解:过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E,作点B作BF⊥x轴,作AF∥x轴,交于点F,连接AC,
解:过点C作CD⊥x轴于点D,过点A作AE⊥x轴于点E,作点B作BF⊥x轴,作AF∥x轴,交于点F,连接AC,∵四边形OABC是平行四边形,
∴OC=AB,OC∥AB,
∴∠COD=∠BAF,
在△COD和△BAF中,
∵
|
∴△COD≌△BAF(AAS),
∴OD=AF,
∵点A的横坐标为2,点B的横坐标为3,
∴AF=1,
∴OD=1,
即点C的横坐标为1,
∵顶点A,C在反比例函数y=
| k |
| x |
∴点A(2,
| k |
| 2 |
∴DE=OE-OD=4-2=2,
∵平行四边形OABC的面积为4,
∴S△OAC=2,
∴S△OAC=S△OCD+S梯形AEDC-S△OAE=S梯形AEDC=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
解得:k=
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:此题考查了反比例函数的意义、全等三角形的判定与性质以及平行四边形的性质.此题难度较大,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列计算错误的是( )
| A、(-5)3÷(-52)=5 | ||||||
B、
| ||||||
C、3-1÷3=
| ||||||
D、
|
 如图,在平面直角坐标系中,反比例函数y=
如图,在平面直角坐标系中,反比例函数y= 如图,在凸四边形ABCD中,AB=BC=BD,∠ABC=80°,则∠ADC等于
如图,在凸四边形ABCD中,AB=BC=BD,∠ABC=80°,则∠ADC等于 如图,已知∠AOB=∠COD=90°,∠AOC=20°45′,则∠AOD=
如图,已知∠AOB=∠COD=90°,∠AOC=20°45′,则∠AOD= 如图,AB∥CD,DB⊥BC,∠1=50°,则∠2的度数等于
如图,AB∥CD,DB⊥BC,∠1=50°,则∠2的度数等于