题目内容
观察下列等式:4×6=24,14×16=224,24×26=624,34×36=1224,…,请你综合上述规律的第n个等式 (不要求化简)
考点:规律型:数字的变化类
专题:
分析:由4×6=24,14×16=224,24×26=624,34×36=1224,…,可以看出两个因数的个位数是4和6,前面数位上的数字相同,所得的积的末尾是24,前面的数字是相同数字和相同数字加1的乘积,由此规律解决问题.
解答:解:4×6=24,
14×16=100×1×(1+1)+24=224,
24×26=100×2×(2+1)+24=624,
34×36=100×3×(3+1)+24=1224,
…
第n个等式:[10(n-1)+4][10(n-1)+6]=100n(n-1)+24.
故答案为:[10(n-1)+4][10(n-1)+6]=100n(n-1)+24.
14×16=100×1×(1+1)+24=224,
24×26=100×2×(2+1)+24=624,
34×36=100×3×(3+1)+24=1224,
…
第n个等式:[10(n-1)+4][10(n-1)+6]=100n(n-1)+24.
故答案为:[10(n-1)+4][10(n-1)+6]=100n(n-1)+24.
点评:此题考查数字的变化规律,找出数字和算式之间的联系,得出规律,解决问题.

练习册系列答案
相关题目
 如图,几何体的左视图是( )
如图,几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
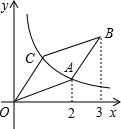 如图,?ABCD的顶点O在原点,顶点A、C在反比例函数
如图,?ABCD的顶点O在原点,顶点A、C在反比例函数 在平面直角坐标系中.已知O坐标原点.以点A为旋转中心,把△ABO顺时针旋转得△ACD,并使BC∥x轴,记旋转转角为x度.∠ABO=y度.则y与x之间满足的函数关系式为
在平面直角坐标系中.已知O坐标原点.以点A为旋转中心,把△ABO顺时针旋转得△ACD,并使BC∥x轴,记旋转转角为x度.∠ABO=y度.则y与x之间满足的函数关系式为