Question

如图，在平面直角坐标系中，反比例函数y=

k

x

（x＞0）的图象在第一象限，矩形OABC的顶点A在y轴负半轴，顶点C在x轴正半轴，且OA=4

3

，AB=6．
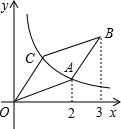
（1）直接写出A、B、C三点的坐标；
（2）将矩形OABC绕顶点O逆时针旋转60°，矩形的两个顶点恰好同时落在反比例函数的图象上，猜想这是哪两个点，并求出此时这两个点的坐标及反比例函数的解析式．

Answer 1

考点：反比例函数图象上点的坐标特征,矩形的性质,坐标与图形变化-旋转

专题：

分析：（1）直接根据矩形的性质即可得出各点坐标；
（2）根据点A在y轴负半轴上可知，将矩形OABC绕顶点O逆时针旋转60°，必然是BC两点落在反比例函数的图象上，过点C′作C′D⊥y轴于点D，由直角三角形的性质求出C′D的长，进而得出C′的坐标，进而得出反比例函数的解析式，在Rt△OAE中求出OC的长，利用待定系数法求出直线OC的解析式，根据平移的性质得出直线A′B′的解析式，进而得出B点坐标．

解答：解：（1）∵四边形ABCD是矩形，OA=4

3

，AB=6，
∴A（0，-4

3

），B（6，-4

3

），C（6，0）；

（2）如图所示，
∵点A在y轴负半轴上，
∴将矩形OABC绕顶点O逆时针旋转60°，B、C两点落在反比例函数的图象上，
过点C′作C′D⊥y轴于点D，
∵OC′=OC=6，∠EOC′=60°，
∴∠DOC′=30°，
∴C′D=3，OD=

OC′2-C′D2

=

62-32

=3

3

，
∴C′（3，3

3

），
∴反比例函数的解析式为y=

9 3

x

，
∵∠AOA′=60°，OA′=OA=4

3

，
∴∠A′OE=30°，
∴OC=

OA′

cos30°

=

4 3

3 2

=8，
设直线OC′的解析式为y=kx（k≠0），
∵C′（3，3

3

），
∴3

3

=3k，解得k=

3

，
∴直线OC′的解析式为y=

3

x，
∵OC′∥A′B′，
∴直线A′B′的解析式为y=

3

x-8

3

，
∴

y= 3 x y= 3 x-8 3

，
解得x=9，y=

3

，
∴B′（9，

3

）．

点评：本题考查的是反比例函数图象上点的坐标特点，涉及到图形旋转的性质、矩形的性质等知识，难度较大．