Question

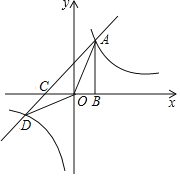
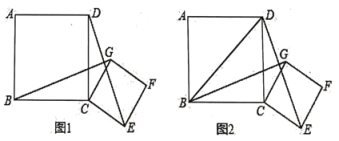
【题目】如图，点是正方形的边延长线一点，连接交于，作，交的延长线于，连接，当时，作于，连接，则的长为（ ）

A.B.C.D.

Answer 1

【答案】C

【解析】

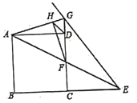
作AP⊥EG于点P，作HM⊥AD，HN⊥CG， 易证∠GAF=∠GCE=45°，进而得：AH=HF，由余角的性质，得∠GAD=∠GFH，得到AMH FNH(AAS)，进而得：四边形HMDN是正方形，设HM=x，则FN=1+x，AM=2-x，列出方程，即可得到答案.

作AP⊥EG于点P，作HM⊥AD，HN⊥CG，

∵，

∴AB=AP，

∵四边形是正方形，

∴AD=AP，

∴AG平分∠CGP，

∵∠PGC-∠GEC=∠GCE，∠PGA-∠GEA=∠GAF，

∴∠GAF=∠GCE=45°，

∵，

∴AH=HF，

∵∠GAD+∠AGF=90°，∠GFH+∠AGF=90°，

∴∠GAD=∠GFH，

在AMH和FNH中，

∵，

∴AMH FNH(AAS)，

∴HM=HN，AM=FN，

∴四边形HMDN是正方形，

∵，

∴，即：，

∴FC=1，

∴DF=2-1=1，

设HM=x，则FN=1+x，AM=2-x，

∴1+x=2-x，解得：x=，

∴DH=.

故选C.