��Ŀ����
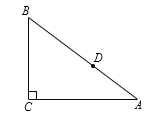
����Ŀ����ͼ����ƽ��ֱ������ϵ�У� AB=AC=10���߶�BC��![]() ���ϣ�BC=12����B������Ϊ����3��0�����߶�AB��
���ϣ�BC=12����B������Ϊ����3��0�����߶�AB��![]() ���ڵ�E����A��AD��BC��D������P��ԭ���������ÿ��3����λ���ٶ���
���ڵ�E����A��AD��BC��D������P��ԭ���������ÿ��3����λ���ٶ���![]() �������˶������˶���ʱ��Ϊ
�������˶������˶���ʱ��Ϊ![]() �룮
�룮
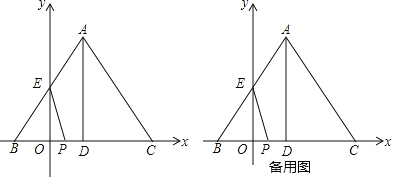
��1������BPE�ǵ���������ʱ����![]() ��ֵ��
��ֵ��
��2������P�˶���ͬʱ����ABC��BΪλ���������ҷŴ��ҵ�C�����˶����ٶ�Ϊÿ��2����λ����ABC�Ŵ��ͬʱ��ADҲ��֮�Ŵ���EPΪֱ����Բ�붯�߶�AD����ֱ������ʱ����![]() ��ֵ�ʹ�ʱ��C�����꣮
��ֵ�ʹ�ʱ��C�����꣮
���𰸡���1��t=![]() ��t=1��t=
��t=1��t=![]() ����2����t=1ʱ��F�붯�߶�AD����ֱ�����У���ʱC��11��0����
����2����t=1ʱ��F�붯�߶�AD����ֱ�����У���ʱC��11��0����
��������
��1���������ֱ��AB�Ľ���ʽ�������ֱ����âٵ�BE��BPʱ���ڵ�EB��EPʱ���۵�PB��PEʱ���ó�t��ֵ���ɣ�
��2�����ȵó���PGF�ס�POE����������Rt��EOP�У�EP2��OP2��EO2���������t��ֵ�Լ�C�����꣮
��1����AB=AC��AD��BC��
��BD=CD=6��
��AB=10����AD=8����A��3��8����
��ֱ��AB�Ľ���ʽΪ��y=kx+b����![]() ��
��
��ã�![]() ��
��
��ֱ��AB�Ľ���ʽΪ��y=![]() x+4��
x+4��
��E��0��4����
��BE=5��
����BPE�ǵ��������������������
����BE=BPʱ��3+3t=5����ã�t=![]() ��
��
����EB=EPʱ��3t=3����ã�t=1��
����PB=PEʱ��
��PB=PE��AB=AC����ABC=��PBE��
���PEB=��ACB=��ABC��
���PBE�ס�ABC��
��![]() ��
��
��![]() ����ã�t=
����ã�t=![]() ��
��
���ϣ�t=![]() ��t=1��t=
��t=1��t=![]() ��
��
��2��������ã�C��9+2t��0����
��BC=12+2t��BD=CD=6+t��OD=3+t��
��FΪEP���е㣬����OF����FH��AD��FG��OP��
��FG��EO��
���PGF�ס�POE��
��PG=OG=![]() t��FG=
t��FG=![]() EO=2����F��
EO=2����F��![]() t��2����
t��2����
��FH=GD=OD��OG=3+t��![]() t=3��
t=3��![]() t��
t��
�ߡ�F�붯�߶�AD����ֱ�����У�FH=![]() EP=3��
EP=3��![]() t��
t��
��Rt��EOP��EP2=OP2+EO2
��4��3��![]() t��2=��3t��2+16
t��2=��3t��2+16
��ã�t1=1��t2=��![]() ����ȥ����
����ȥ����
����t=1ʱ��F�붯�߶�AD����ֱ�����У���ʱC��11��0����


 ��ĩ100�ִ��غ�������ϵ�д�
��ĩ100�ִ��غ�������ϵ�д� Сѧ�������Ծ�ϵ�д�
Сѧ�������Ծ�ϵ�д�