题目内容
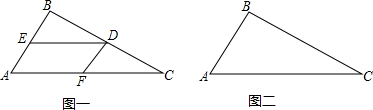
如图,在△ABC中,∠B为钝角,∠A=60°,D是射线BC上的一点,过D点作DE∥AC交射线BA于点E,F为射线AC上一点,∠FDC=∠B.
(1)如图一,当点D在线段BC上时,求∠EDF的度数;
(2)当点D在线段BC的延长线上时,请在图二中画出图形.此时∠EDF的度数是否发生变化?若有变化,求出∠EDF的度数;若无变化,说明理由.
(1)如图一,当点D在线段BC上时,求∠EDF的度数;
(2)当点D在线段BC的延长线上时,请在图二中画出图形.此时∠EDF的度数是否发生变化?若有变化,求出∠EDF的度数;若无变化,说明理由.

考点:平行线的判定与性质
专题:
分析:(1)由∠FDC=∠B,得到AE∥DF;而DE∥AC,故可证明四边形AFDE为平行四边形,即可解决问题.
(2)运用与(1)中类似的方法,证明四边形AFDE为平行四边形,即可解决问题.
(2)运用与(1)中类似的方法,证明四边形AFDE为平行四边形,即可解决问题.
解答:解:(1)如图1,∵∠FDC=∠B,
∴AE∥DF,而DE∥AC,
∴四边形AFDE是平行四边形,
∴∠EDF=∠A=60°.

(2)∠EDF的度数会发生变化;解析如下:
如图2,∵∠FDC=∠B,
∴AE∥DF,而DE∥AC,
∴四边形AFDE是平行四边形,
∴∠EDF=∠EAF=180°-60°=120°,
即∠EDF的度数会发生变化,为120°.

∴AE∥DF,而DE∥AC,
∴四边形AFDE是平行四边形,
∴∠EDF=∠A=60°.

(2)∠EDF的度数会发生变化;解析如下:
如图2,∵∠FDC=∠B,
∴AE∥DF,而DE∥AC,
∴四边形AFDE是平行四边形,
∴∠EDF=∠EAF=180°-60°=120°,
即∠EDF的度数会发生变化,为120°.

点评:该题主要考查了平行线的判定及其性质的应用问题;解题的关键是深刻分析、大胆猜测、合情推理、科学论证.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,已知,PM=PN,EQ∥MN,MQ为∠PMN的平分线,且∠MQN=72°,则图中的等腰△有( )
如图,已知,PM=PN,EQ∥MN,MQ为∠PMN的平分线,且∠MQN=72°,则图中的等腰△有( )| A、2个 | B、3个 | C、4个 | D、5个 |
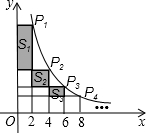 如图,在函数y=
如图,在函数y=