题目内容
10.一次函数y=-$\frac{3}{5}x+2$的图象与x轴交点坐标( )| A. | (0,2) | B. | ($\frac{10}{3}$,0) | C. | (-$\frac{10}{3}$,0) | D. | (2,0) |
分析 令一次函数解析式中y=0,可得出关于x的一元一次方程,解方程即可得出结论.
解答 解:令一次函数y=-$\frac{3}{5}$x+2中x=0,则有0=-$\frac{3}{5}$x+2,
解得:x=$\frac{10}{3}$.
即一次函数y=-$\frac{3}{5}$x+2的图象与x轴交点坐标为($\frac{10}{3}$,0).
故选B.
点评 本题考查了一次函数图象上点的坐标特征,解题的关键是将y=0代入一次函数解析式求出x的值.本题属于基础题,难度不大,解决该题型题目时,代入x=0(或y=0)求出y(或x)的值是关键.

练习册系列答案
相关题目
5.要得到y=2kx+3的图象,向左平移3个单位,再向上平移2个单位恰好经过点(-2,1),则k的值是( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
2.某班有36人参加义务植树劳动,他们分为植树和挑水两组,要求挑水人数是植树人数的2倍,设有x人挑水,y人植树,则下列方程组中正确的是( )
| A. | $\left\{\begin{array}{l}{2x+y=6}\\{x=2y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+2y=36}\\{y=2x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=36}\\{x=2y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=36}\\{y=2x}\end{array}\right.$ |
 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )



 将等边△CBA绕点C顺时针旋转∠α得到△CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是120°.
将等边△CBA绕点C顺时针旋转∠α得到△CB′A′,使得B,C,A′三点在同一直线上,如图所示,则∠α的大小是120°. 如图,在四边形ABCD中,已知AB∥CD,AB=CD,在不添加任何辅助线的前提下,要想该四边形成为菱形,只需再添加上的一个条件是AB=AD或AC⊥BD.
如图,在四边形ABCD中,已知AB∥CD,AB=CD,在不添加任何辅助线的前提下,要想该四边形成为菱形,只需再添加上的一个条件是AB=AD或AC⊥BD.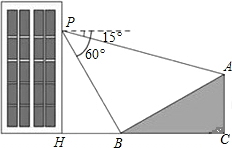 如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角∠APQ为15°,山脚B处的俯角∠BPQ为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角∠APQ为15°,山脚B处的俯角∠BPQ为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.