题目内容
20.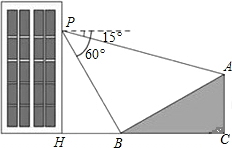 如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角∠APQ为15°,山脚B处的俯角∠BPQ为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.
如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角∠APQ为15°,山脚B处的俯角∠BPQ为60°,已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC.(1)求出山坡坡角(∠ABC)的大小;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732).
分析 (1)根据俯角以及坡度的定义即可求解;
(2)在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
解答 解:(1)∵tan∠ABC=1:$\sqrt{3}$,
∴∠ABC=30°; (2)由题意得:∠PBH=60°,
(2)由题意得:∠PBH=60°,
∵∠ABC=30°,
∴∠ABP=90°,
又∵∠APB=45°,
∴△PAB为等腰直角三角形,
在直角△PHB中,PB=$\frac{PH}{sin∠PBH}$=$\frac{30}{\frac{\sqrt{3}}{2}}$=20$\sqrt{3}$米.
在直角△PBA中,AB=PB=20$\sqrt{3}$≈34.6米.
点评 本题主要考查了解直角三角形的应用-俯角的问题以及坡度的定义,正确利用三角函数是解题的关键.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
10.一次函数y=-$\frac{3}{5}x+2$的图象与x轴交点坐标( )
| A. | (0,2) | B. | ($\frac{10}{3}$,0) | C. | (-$\frac{10}{3}$,0) | D. | (2,0) |
11.几个人共同种一批树苗,如果每人种10棵,则剩下6棵树苗未种:如果每人种12棵,则缺6棵树苗,求这批树苗有多少棵?设有x棵树苗,则下列方程为( )
| A. | 10x+6=12x-6 | B. | 10x-6=12x+6 | C. | $\frac{x-6}{10}=\frac{x+6}{12}$ | D. | $\frac{x+6}{10}=\frac{x-6}{12}$ |
12.下列计算正确的是( )
| A. | a2+a2=a4 | B. | (a2)3=a5 | C. | a+2=2a | D. | (ab)3=a3b3 |
9.拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克,这个数据用科学记数法表示为( )
| A. | 0.5×1011千克 | B. | 50×109千克 | C. | 5×109千克 | D. | 5×1010千克 |