题目内容
3.计算:($\frac{1}{3}$)-1-$\sqrt{12}$+2tan60°-(2-$\sqrt{3}$)0.分析 原式利用零指数幂、负整数指数幂法则,二次根式性质,以及特殊角的三角函数值计算即可得到结果.
解答 解:原式=3-2$\sqrt{3}$+2$\sqrt{3}$-1
=2.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13. 如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于( )
如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于( )
 如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于( )
如图,直线AB∥CD,∠B=50°,∠C=40°,则∠E等于( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
14.关于抛物线y=x2-2x+1,下列说法错误的是( )
| A. | 开口向上 | B. | 与x轴有两个重合的交点 | ||
| C. | 对称轴是直线x=1 | D. | 当x>1时,y随x的增大而减小 |
18.下列长度的三根小木棒能构成三角形的是( )
| A. | 2cm,3cm,5cm | B. | 7cm,4cm,2cm | C. | 3cm,4cm,8cm | D. | 3cm,3cm,4cm |
3.x4-9因式分解正确的是( )
| A. | (x2+3)(x2-3) | B. | (x2+3)(x+3)(x-3) | C. | (x2+3)(x+$\sqrt{3}$)(x-$\sqrt{3}$) | D. | (x2+3)(x-$\sqrt{3}$) |
10.一次函数y=-$\frac{3}{5}x+2$的图象与x轴交点坐标( )
| A. | (0,2) | B. | ($\frac{10}{3}$,0) | C. | (-$\frac{10}{3}$,0) | D. | (2,0) |
7.已知数据$\frac{1}{2}$,-6,$\frac{1}{3}$,π,$\sqrt{2}$,其中有理数出现的频率是( )
| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
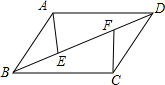 如图所示,点E,F是平行四边形ABCD对角线BD上的点,BF=DE,求证:AE=CF.
如图所示,点E,F是平行四边形ABCD对角线BD上的点,BF=DE,求证:AE=CF.