题目内容
3.在高为60米的小山上,测得山底一座楼房的顶端和底部的俯角分别为30°和60°,则这座楼房的高为40米.分析 作CE⊥AB,根据∠DAB可以求得CE的长,根据CE即可求得AE的长,根据CD=BE=AB-AE即可解题.
解答 解:作CE⊥AB,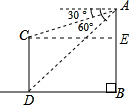
∵∠DAB=90°-60°=30°,
tan30°=$\frac{\sqrt{3}}{3}$,
∴CE=BD=$\frac{\sqrt{3}}{3}$×AB=20$\sqrt{3}$(米),
∵∠ACE=30°,
∴AE=CEtan30°=20$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=20(米),
∴CD=BE=AB-AE=60-20=40(米),
故答案为:40米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据俯角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
14.下列命题中假命题是( )
| A. | 平分弦的半径垂直于弦 | |
| B. | 垂直平分弦的直线必经过圆心 | |
| C. | 垂直于弦的直径平分这条弦所对的弧 | |
| D. | 平分弧的直径垂直平分这条弧所对的弦 |
18.计算:752-252=( )
| A. | 50 | B. | 500 | C. | 5000 | D. | 7100 |
8.下表是我省11个地市5月份某日最高气温(℃)的统计结果:
该日最高气温的极差和平均数分别是( )
| 乐山 | 眉山 | 西昌 | 成都 | 德阳 | 绵阳 | 广安 | 南充 | 宜宾 | 广汉 | 遂宁 |
| 28 | 28 | 31 | 28 | 27 | 28 | 27 | 26 | 30 | 28 | 27 |
| A. | 31℃,28℃ | B. | 26℃,28℃ | C. | 5℃,27℃ | D. | 5℃,28℃ |
15.某工地因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案.
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型机 | 100 | 60 |
| 乙型机 | 120 | 80 |
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案.
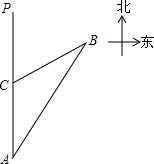 一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.
一船以每小时36海里的速度向正北航行到A处,发现它的北偏东30°方向上有一灯塔B,船继续向北航行40分钟后到达C处,发现灯塔B在北偏东60°方向上,求此船与灯塔的距离.