题目内容
1.先化简,再求值:($\frac{1}{x-1}$-$\frac{1}{x+1}$)•$\frac{x^2-1}{x}$,其中x=$\sqrt{3}$-1.分析 根据分式混合运算法则先化简后代入即可.
解答 解:原式=$\frac{x+1-x+1}{(x-1)(x+1)}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{2}{x}$.
当x=$\sqrt{3}$-1时,原式=$\frac{2}{\sqrt{3}-1}$=$\frac{2(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}$=$\sqrt{3}+1$.
点评 本题考查分式的混合运算法则、分母有理化等知识,熟练掌握分式的混合运算法则是解题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
12.随着“双11”从PC走向APP,网上购物变得更为便捷.估计今年淘宝“双11”将创造新的网购交易记录,总销量额可能会达到637亿.数据“637亿元”用科学记数法可表示为( )
| A. | 637×108元 | B. | 63.7×109元 | C. | 6.4×1010元 | D. | 6.37×1010元 |
9.2015的相反数是( )
| A. | $\frac{1}{2015}$ | B. | -2015 | C. | 2015 | D. | -$\frac{1}{2015}$ |
13.下列说法中正确的是( )
| A. | 方程$\sqrt{2}$x-$\sqrt{3}$=x是无理方程 | B. | 方程$\sqrt{{x}^{2}+1}$=1没有实数根 | ||
| C. | 方程$\sqrt{-x}$=2没有实数根 | D. | 方程$\sqrt{x}$=-x的根是x=0 |
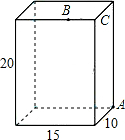 如图,一个无盖的长方体盒子的长为15cm,宽为10cm,高为20cm,点B离点C的距离为
如图,一个无盖的长方体盒子的长为15cm,宽为10cm,高为20cm,点B离点C的距离为 如图,已知抛物线y=ax2+bx+c过点A(-1,0),B(4,0),C(-2,-3)三点,与y轴相交于点D.
如图,已知抛物线y=ax2+bx+c过点A(-1,0),B(4,0),C(-2,-3)三点,与y轴相交于点D.