题目内容
15.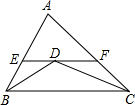 如图,△ABC中,AB=5,AC=8,BD,CD分别平分∠ABC,∠ACB,过点D作直线平行于BC,交AB,AC于E,F,则△AEF的周长为( )
如图,△ABC中,AB=5,AC=8,BD,CD分别平分∠ABC,∠ACB,过点D作直线平行于BC,交AB,AC于E,F,则△AEF的周长为( )| A. | 12 | B. | 13 | C. | 14 | D. | 18 |
分析 根据平行线的性质得到∠EDB=∠DBC,∠FDC=∠DCB,根据角平分线的性质得到∠EBD=∠DBC,∠FCD=∠DCB,等量代换得到∠EDB=∠EBD,∠FDC=∠FCD,于是得到ED=EB,FD=FC,即可得到结果.
解答 解:∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB,
∵△ABC中,∠ABC和∠ACB的平分线相交于点D,
∴∠EBD=∠DBC,∠FCD=∠DCB,
∴∠EDB=∠EBD,∠FDC=∠FCD,
∴ED=EB,FD=FC,
∵AB=5,AC=8,
∴△AEF的周长为:AE+EF+AF=AE+ED+FD+AF=AE+EB+FC+AF=AB+AC=5+8=13.
故选B.
点评 此题考查了等腰三角形的判定与性质.此题难度适中,注意证得△BDE与△CDF是等腰三角形是解此题的关键.

练习册系列答案
相关题目
6.一个三角形的周长是偶数,其中的两条边长分别是4和7,满足上述条件的三角形(三角形的边长均为整数)的个数为( )
| A. | 1个 | B. | 3个 | C. | 5个 | D. | 7个 |
7.如果a,b表示两个实数,那么下列命题正确的是( )
| A. | 若a2=b2,则a=b | B. | 若a<b,则$\sqrt{{a}^{2}}<\sqrt{{b}^{2}}$ | C. | 若$\root{3}{a}$=$\root{3}{b}$,则$\sqrt{a}=\sqrt{b}$ | D. | 若a>b,则$\root{3}{a}$$>\root{3}{b}$ |
4.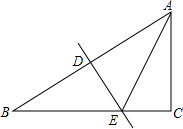 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )
 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )| A. | 16 | B. | 14 | C. | 12 | D. | 10 |
 如图,在Rt△ABC中,∠ACB=90°,AC=20,BC=15,求AB的长.
如图,在Rt△ABC中,∠ACB=90°,AC=20,BC=15,求AB的长.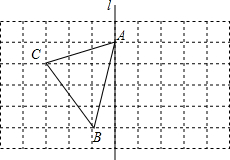 如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.