题目内容
10．如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（a，b），则经过第2014次变换后所得A点坐标是（ ）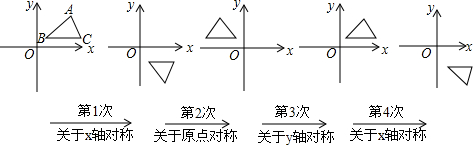
| A． | （a，-b） | B． | （-a，-b） | C． | （-a，b） | D． | （a，b） |
分析 利用已知得出图形的变换规律，进而得出经过第2014次变换后所得A点坐标与第1次变换后的坐标相同求出即可．
解答 解：∵在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，
∴对应图形3次循环一周，
∵2014÷3=671…1，
∴经过第2014次变换后所得A点坐标与第1次变换后的坐标相同，故其坐标为：（a，b）．
故选：D．
点评 此题主要考查了关于坐标轴以及原点对称点的性质，得出A点变化规律是解题关键．
练习册系列答案
相关题目
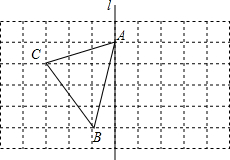如图，在长度为1个单位长度的小正方形组成的长方形中，点A，B，C在小正方形的顶点上．
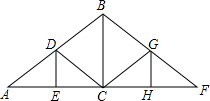如图是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC，DC垂直于横梁AC，AB=8m，∠A=30°，立柱BC，DE要多长？
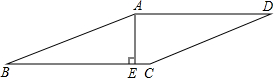如图，在菱形ABCD中，已知AE⊥BC于点E，EC=1，且AE：BE=5：2，求四边形ABCD的周长．
20．下列计算正确的是（ ）
| A． | $\root{3}{-8}$=-2 | B． | $\sqrt{36}$=±6 | C． | $\sqrt{3}$$+\sqrt{2}$=$\sqrt{5}$ | D． | $\sqrt{{a}^{2}}$=a |