题目内容
8.设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.(1)一次函数y=-x+7是闭区间[3,4]上的“闭函数”吗?请判断,并说明理由;
(2)若二次函数y=x2-4x-1是闭区间[a,b]上的“闭函数”,a<2<b,求实数a,b的值.
分析 (1)分别计算出自变量为3或4时的函数值,然后根据闭函数的定义进行判断;
(2)首先求出二次函数y=x2-4x-1最小值,结合闭函数的定义以及二次函数的增减性即可求出a和b的值.
解答 解:(1)x=3时,y=-x+7=4;当x=4时,y=-x+7=3,
所以y=-x+7是闭区间[3,4]上的“闭函数”;
(2)∵二次函数解析式为y=x2-4x-1,
∴y=(x-2)2-5,
∴当x=2时,y有最小值为-5,
∵当a<2<b时,二次函数y=x2-4x-1是闭区间[a,b]上的“闭函数”,
∴a=-5,
∴b2-4b-1=b,
∴b=$\frac{5+\sqrt{29}}{2}$.
点评 本题主要考查了二次函数的性质以及一次函数的性质的知识,解答本题的关键是理解闭区间以及闭函数的意义,此题难度不大.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
19.若实数a,b满足a+b2=2,则a2+6b2的最小值为( )
| A. | -3 | B. | 3 | C. | -4 | D. | 4 |
16.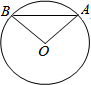 如图,∠AOB=110°,弦AB所对的圆周角为( )
如图,∠AOB=110°,弦AB所对的圆周角为( )
 如图,∠AOB=110°,弦AB所对的圆周角为( )
如图,∠AOB=110°,弦AB所对的圆周角为( )| A. | 55° | B. | 55°或70° | C. | 55°或125° | D. | 55°或110° |