题目内容
2.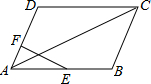 如图,在?ABCD中,E是边AB的中点,F是边AD上一点,AF=$\frac{1}{2}$FD,连结EF交AC于点G,若AC=10,则AG的长为2.
如图,在?ABCD中,E是边AB的中点,F是边AD上一点,AF=$\frac{1}{2}$FD,连结EF交AC于点G,若AC=10,则AG的长为2.
分析 首先求证出EO∥BC,得到EO=$\frac{1}{2}$BC,然后根据平行线的性质求证出△AFG∽△OEG.进而得到$\frac{AG}{OG}=\frac{AF}{OE}$,求出AG,即可得到结论.
解答 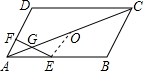 解:在?ABCD中,
解:在?ABCD中,
设AC的中点为O,连接EO,又E是AB的中点,
∴EO∥BC,EO=$\frac{1}{2}$BC=$\frac{1}{2}$AD,
又AD∥BC,
∴AF∥EO,
∴△AFG∽△OEG,
∴$\frac{AG}{OG}=\frac{AF}{OE}$=$\frac{\frac{1}{3}}{\frac{1}{2}}=\frac{2}{3}$,
∵AC=10,
∴AG=2,
故答案为:2
点评 本题主要考查了平行四边形的性质,全等三角形的判定及线段的比例问题,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.若代数式$\frac{3}{\sqrt{x-1}}$有意义,则实数x的取值范围是( )
| A. | x<1 | B. | x≥1 | C. | x≤1 | D. | x>1 |
10.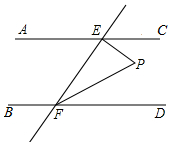 如图,若AC∥BD,EF与AC、BD分别相交于E、F,∠EFD的平分线FP与EP相交于点P.
如图,若AC∥BD,EF与AC、BD分别相交于E、F,∠EFD的平分线FP与EP相交于点P.
(1)探求∠AEF与∠EFP的数量关系并说明理由;
(2)若EP⊥EF,∠AEF=45°,求∠P的度数.
 如图,若AC∥BD,EF与AC、BD分别相交于E、F,∠EFD的平分线FP与EP相交于点P.
如图,若AC∥BD,EF与AC、BD分别相交于E、F,∠EFD的平分线FP与EP相交于点P.(1)探求∠AEF与∠EFP的数量关系并说明理由;
(2)若EP⊥EF,∠AEF=45°,求∠P的度数.
14.圆有( )条对称轴.
| A. | 1 | B. | 2 | C. | 4 | D. | 无数条 |
12.下列式子一定是二次根式的是( )
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\sqrt{x}$ | C. | $\sqrt{x+2}$ | D. | $\sqrt{{x^2}-2}$ |
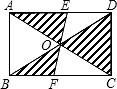 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=4cm,BC=6cm,则图中阴影部分的面积为12cm2.
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=4cm,BC=6cm,则图中阴影部分的面积为12cm2.