题目内容
 如图,在正方形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE),△AEF∽△EFC吗?若相似,请证明;若不相似,请说明理由.若ABCD为矩形呢?
如图,在正方形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE),△AEF∽△EFC吗?若相似,请证明;若不相似,请说明理由.若ABCD为矩形呢?考点:相似三角形的判定
专题:
分析:根据线段中点的定义可得AE=DE,求出∠AEF=∠DCE,利用两组角对应相等的两个三角形相似求出△AEF和△DCE相似,根据相似三角形对应边成比例可得
=
=
,然后求出
=
,再根据两边对应成比例,夹角相等,两三角形相似求解即可;矩形时同理可求.
| AF |
| DE |
| AE |
| CD |
| EF |
| EC |
| AF |
| AE |
| EF |
| EC |
解答:解:∵E为AD的中点,
∴AE=DE,
∵EF⊥EC,
∴∠AEF+∠DEC=90°,
∠DCE+∠DEC=90°,
∴∠AEF=∠DCE,
又∵∠A=∠D=90°,
∴△AEF∽△DCE,
∴
=
=
,
∴
=
,
又∵∠A=∠CEF=90°,
∴△AEF∽△EFC;
ABCD为矩形时,同理可得△AEF∽△DCE,
∴
=
=
,
∴
=
,
又∵∠A=∠CEF=90°,
∴△AEF∽△EFC.
∴AE=DE,
∵EF⊥EC,
∴∠AEF+∠DEC=90°,
∠DCE+∠DEC=90°,
∴∠AEF=∠DCE,
又∵∠A=∠D=90°,
∴△AEF∽△DCE,
∴
| AF |
| DE |
| AE |
| CD |
| EF |
| EC |
∴
| AF |
| AE |
| EF |
| EC |
又∵∠A=∠CEF=90°,
∴△AEF∽△EFC;
ABCD为矩形时,同理可得△AEF∽△DCE,
∴
| AF |
| DE |
| AE |
| CD |
| EF |
| EC |
∴
| AF |
| AE |
| EF |
| EC |
又∵∠A=∠CEF=90°,
∴△AEF∽△EFC.
点评:本题考查了相似三角形的判定,正方形的性质,矩形的性质,熟练掌握相似三角形的判定与性质是解题的关键.

练习册系列答案
相关题目
一元二次方程x2-3x-5=0中二次项系数、一次项系数、常数项分别为( )
| A、1、3、5 |
| B、1、3、-5 |
| C、1、-3、-5 |
| D、1、-3、5 |
 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.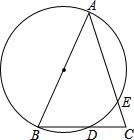 如图,在△ABC中,AB=AC,过A、B两点的圆交AC于点E,交BC于点D,且D为BC的中点.
如图,在△ABC中,AB=AC,过A、B两点的圆交AC于点E,交BC于点D,且D为BC的中点.