题目内容
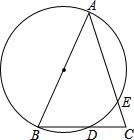 如图,在△ABC中,AB=AC,过A、B两点的圆交AC于点E,交BC于点D,且D为BC的中点.
如图,在△ABC中,AB=AC,过A、B两点的圆交AC于点E,交BC于点D,且D为BC的中点.(1)求证:AB为此圆的直径;
(2)如果点E是
 |
| AD |
考点:圆周角定理,等腰三角形的性质
专题:
分析:(1)连接AD,AB=AC,求出∠ADB=90°,判断出AB为此圆的直径;
(2)点E是
的中点,
=
判断出∠1=∠4=∠3,得到∠ABC=∠C=∠BAC,判断出△ABC是等边三角形.
(2)点E是
 |
| AD |
 |
| AE |
 |
| DE |
解答:
 解:(1)如图1,连接AD,
解:(1)如图1,连接AD,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∴AB为此圆的直径;
(2)如图2,
∵点E是
的中点,
∴
=
,
∴∠1=∠4=∠3,
又∵∠1=∠2,
∴∠1+∠2=∠3+∠4,
∴∠ABC=∠C=∠BAC,
∴△ABC是等边三角形.

 解:(1)如图1,连接AD,
解:(1)如图1,连接AD,∵AB=AC,D为BC的中点,
∴AD⊥BC,
∴∠ADB=90°,
∴AB为此圆的直径;
(2)如图2,
∵点E是
 |
| AD |
∴
 |
| AE |
 |
| DE |
∴∠1=∠4=∠3,
又∵∠1=∠2,
∴∠1+∠2=∠3+∠4,
∴∠ABC=∠C=∠BAC,
∴△ABC是等边三角形.
点评:本题考查了圆周角定理和等腰三角形的性质,作出辅助线是解题的关键.

练习册系列答案
相关题目

 如图,在正方形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE),△AEF∽△EFC吗?若相似,请证明;若不相似,请说明理由.若ABCD为矩形呢?
如图,在正方形ABCD中,E为AD的中点,EF⊥EC交AB于F,连接FC(AB>AE),△AEF∽△EFC吗?若相似,请证明;若不相似,请说明理由.若ABCD为矩形呢?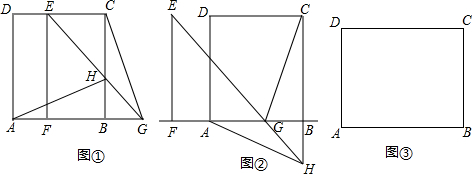
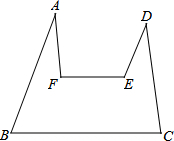 如图,顺次连结A、B、C、D、E、F,若∠F=∠A+∠B.求证:∠E=∠D+∠C.
如图,顺次连结A、B、C、D、E、F,若∠F=∠A+∠B.求证:∠E=∠D+∠C.